Chapter No. 03 - Permutation and Combination

Exercise 3.1

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9 Q.10 Q.11 Q.12 Q.13 Q.14

Q.1 A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl or a boy?

There are 30 boys and 20 girls.

A teacher can select any boy as a class monitor from 30 boys in 30 different ways and he can select any girl as a class monitor from 20 girls in 20 different ways.

∴ by the fundamental principle of addition, the total number of ways a teacher can select a class monitor

= 30 + 20 = 50

Hence, there are 50 different ways to select a class monitor.

Q.2 A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?

A signal is generated from 2 flags and there are 4 flags of different colours available.

∴ 1^st flag can be any one of the available 4 flags.

∴ It can be selected in 4 ways.

Now, 2^nd flag is to be selected for which 3 flags are available for a different signal.

∴ 2^nd flag can be anyone from these 3 flags.

∴ It can be selected in 3 ways.

∴ By using fundamental principle of multiplication, total no. of ways a signal can be generated

= 4 × 3

= 12

∴ 12 different signals can be generated.

Q.3 How many two letter words can be formed using letters from the word SPACE, when repetition of letters

i. is allowed ?

Number of letters in the word 'SPACE' = 5

In 2-lettered words, both the letters can be selected in 5 different ways, if repetitions of the letters are allowed.

∴ by fundamental principle of multiplication, the total number of 2-lettered words

= 5 × 5

= 25

ii. is not allowed ?

Two-letter word is to be formed out of the letters of the word SPACE.

When repetition of the letters is not allowed

1^st letter can be selected in 5 ways

2^nd letter can be selected in 4 ways

∴ By using fundamental principle of multiplication, total number of 2-letter words

= 5 × 4

= 20

Q.4 How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits

i. is allowed ?

A 3-digit number has 3 places which from left to right are hundred's place, ten's place, and unit's place.

Zero cannot be in the hundred's place. Hence, hundred's place can be filled in by anyone of the 4 non-zero digits 1, 3, 5, 6. Thus hundred's places can be filled in 4 ways.

Since repetition of digits is allowed, the ten's place and unit's place can be filled by anyone of the given 5 digits i.e., ten's place and unit's place can be filled in 5 different ways each.

∴ by fundamental principle of multiplication, the total number of 3-digit numbers formed

= 4 × 5 × 5

= 100

ii. is not allowed ?

Three-digit number is to be formed from the digits 0, 1, 3, 5, 6

When repetition of digits is not allowed 100’s place digit should be a non zero number.

Hence, it can be any one from digits 1, 3, 5, 6

∴ 100’s place digit can be selected in 4 ways

10’s and unit’s place digit can be zero

But digits can’t be repeated

∴ 10’s place digit can be selected in 4 ways and unit’s place digit can be selected in 3 ways

∴ By using fundamental principle of multiplication, total number of two-digit numbers

= 4 × 4 × 3

= 48

Q.5 How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?

A 3-digit number has three places which from left to right are hundred's place, ten's place and unit's place.

Here we have to form 3-digit numbers using the digits 2, 3, 4, 5, 6.

The hundred's place can be filled in by using any one of the given 5 digits in 5 ways.

Since, repetition of digits is allowed each ten's place and unit's place can be filled in by any one of the given 5 digits in 5 ways.

∴ by fundamental principle of multiplication, the total number of 3-digit numbers

= 5 × 5 × 5

= 125.

Q.6 A letter lock contains 3 rings, each ring containing 5 different letters. Determine the maximum number of false trials that can be made before the lock is opened?

Since there are 3 rings each containing 5 different letters.

∴ each ring can be adjusted in 5 different ways,

i.e., m = 5, n = 5, p = 5

∴ by the fundamental principle, 3 rings can be arranged in

= m × n × p

= 5 × 5 × 5

= 125 ways

Out of these 125 trials only one trial is successful to open the lock.

Hence, the maximum number of false trials

= 125 − 1

= 124

Q.7 In a test, 5 questions are of the form 'state, true or false'. No student has got all answers correct. Also, the answer of every student is different. Find the number of students appeared for the test.

True/false questions can be answered in 2 ways either by making it true or false.

∴ each of the 5 questions can be answered in 2 different ways.

∴ total number of different sequences of answers

2⁵ = 2 × 2 × 2 × 2 × 2 = 32

Out of these one sequence is of correct answers and no student has written all correct answers.

Hence, the maximum number of students in the class

= 32 – 1

= 31

Q.8 How many numbers between 100 and 1000 have 4 in the units place?

Numbers between 100 and 1000 are 3-digit numbers.

A 3-digit number is to be formed from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 where unit place digit is 4.

Since Unit’s place digit is 4.

∴ it can be selected in 1 way only.

10’s place digit can be selected in 10 ways. For 3-digit number 100’s place digit should be a non-zero number.

∴ 100’s place digit can be selected in 9 ways.

∴ By using fundamental principle of multiplication, total numbers between 100 and 1000 which have 4 in the units place

= 1 × 10 × 9

= 90

Q.9 How many numbers between 100 and 1000 have the digit 7 exactly once?

Between 100 and 1000 we have all 3-digit numbers and digits used are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Digit 7 can be placed either in unit's place or in ten's place or in hundred's place.

(i) Digit 7 in unit's place :

Unit's place can be filled in only in 1 way.

Ten's place can be filled in by remaining 9 digits in 9 different ways.

Hundred's place can be filled in by (except '0') remaining 8 digits in 8 different ways.

∴ the total numbers between 100 and 1000 with 7 at unit's place

= 8 × 9 × 1

= 72

(ii) Digit 7 in ten's place :

Unit's place can be filled in by remaining 9 digits (except 7) in 9 different ways.

Ten's place can be filled in by 7 in 1 way only.

Hundred's place can be filled in by remaining 8 digits (except 0 and 7) in 8 different ways .

∴ the total numbers between 100 and 1000 with 7 at ten's place

= 8 × 1 × 9

= 72

(iii) Digit 7 in hundred's place :

Unit's place can be filled in by remaining 9 digits (except 6) in 9 different ways.

Ten's place can be filled in by remaining 9 digits (except 7) in 9 different ways.

Hundred's place can be filled in by digit 7 in only 1 way.

∴ the total numbers between 100 and 1000 with 7 at hundred's place

= 1 × 9 × 9

= 81

Hence, there are 72 + 72 + 81 = 225 numbers between 100 and 1000 such that exactly one of the digits is 7.

Q.10 How many four digit numbers will not exceed 7432 if they are formed using the digits 2, 3, 4, 7 without repetition ?

Between any set of digits, greatest number is possible when digits are arranged in descending order.

∴ 7432 is the greatest number, formed from the digits 2, 3, 4, 7.

∴ Since a 4-digit number is to be formed from the digits 2, 3, 4, 7, where repetition of digit is not allowed.

∴ 1000’s place digit can be selected in 4 ways.

100’s place digit can be selected in 3 ways.

10’s place digit can be selected in 2 ways.

Unit’s place digit can be selected in 1 way.

∴ Total number of numbers not exceeding 7432 that can be formed with the digits 2, 3, 4, 7

= Total number of four digit numbers possible from the digits 2, 3, 4, 7

= 4 × 3 × 2 × 1

= 24

Q.11 If numbers are formed using digits 2, 3, 4, 5, 6 without repetition, how many of them will exceed 400 ?

Digits are 2, 3, 4, 5, 6.

We have to form the numbers greater than 400.

The repetition of digits is not allowed. The numbers greater than 400 may be of

(i) 3-digit numbers:

For 3-digit numbers greater than 400, hundred's place can be filled either by 4 or 5 or 6.

Hundred's place can be filled by using 4 or 5 or 6 in 3 different ways.

The ten's and unit's place can be filled by remaining digits in 4 and 3 ways respectively.

∴ total number of 3-digit numbers greater than 400

= 3 × 4 × 3

= 36

(ii) 4-digit numbers:

The thousand's place can be filled by anyone of the given 5 digits in 5 different ways.

Since repetition of digits is not allowed, the hundred's place, ten's place, and unit's place can be filled by remaining digits in 4, 3, and 2 ways respectively.

∴ total number of 4-digit numbers

= 5 × 4 × 3 × 2

= 120

(iii) 5-digit numbers:

The ten thousand's place can be filled by anyone of the given 5 digits in 5 different ways.

Since repetition of digits is not allowed, the thousand's place, hundred's place, ten's place, and unit's place can be filled by remaining digits in 4, 3, 2, and 1 way respectively.

∴ total number of 5-digit numbers

= 5 × 4 × 3 × 2 × 1

= 120

Thus, the total numbers greater than 400

= 36 + 120 + 120

= 276

Q.12 How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated ?

Case I: 2-digit numbers more than 13, less than 20, formed from the digits 0, 1, 2, 5, 7, 8

Number of such numbers = 3

Case II: 2-digit numbers more than 20 formed from 0, 1, 2, 5, 7, 8

Using multiplication principle, the number of such numbers (repetition allowed)

= 4 × 6

= 24

Case III: 3-digit numbers formed from 0, 1, 2, 5, 7, 8

Using multiplication principle, the number of such numbers (repetition allowed)

= 5 × 6 × 6

= 180

All cases are mutually exclusive.

Required number = 3 + 24 + 180 = 207

Q.13 A school has three gates and four staircases from the first floor to the second floor. How many ways does a student have to go from outside the school to his classroom on the second floor ?

3 gates to enter the school.

4 staircases to go from the first floor to the second floor.

∴ the number of ways of going to the classroom is

$= (\begin{matrix} The number of ways \\ to enter the school \end{matrix}) \times (\begin{matrix} The number of ways to \\ go to the second floor \end{matrix})$

= 3 × 4

= 12 ways

Q.14 How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated ?

For a number to be divisible by 5,

Unit’s place digit should be 0 or 5.

Case I: when unit’s place is 0

Unit’s place digit can be selected in 1 way.

10’s place digit can be selected in 5 ways.

100’s place digit can be selected in 4 ways.

1000’s place digit can be selected in 3 ways.

10000’s place digit can be selected in 2 ways.

∴ total number of numbers = 1 × 5 × 4 × 3 × 2 = 120

Case II: when unit’s place is 5

Unit’s place digit can be selected in 1 way

10000’s place should be a non-zero number

∴ It can be selected in 4 ways

1000’s place digit can be selected in 4 ways.

100’s place digit can be selected in 3 ways.

10’s place digit can be selected in 2 ways.

∴ total number of numbers = 1 × 4 × 4 × 3 × 2 = 96

∴ Required number = 120 + 96 = 216

Q.14 How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated ?

For a number to be divisible by 5,

Unit’s place digit should be 0 or 5.

Case I: when unit’s place is 0

Unit’s place digit can be selected in 1 way.

10’s place digit can be selected in 5 ways.

100’s place digit can be selected in 4 ways.

1000’s place digit can be selected in 3 ways.

10000’s place digit can be selected in 2 ways.

∴ total number of numbers = 1 × 5 × 4 × 3 × 2 = 120

Case II: when unit’s place is 5

Unit’s place digit can be selected in 1 way

10000’s place should be a non-zero number

∴ It can be selected in 4 ways

1000’s place digit can be selected in 4 ways.

100’s place digit can be selected in 3 ways.

10’s place digit can be selected in 2 ways.

∴ total number of numbers = 1 × 4 × 4 × 3 × 2 = 96

∴ Required number = 120 + 96 = 216

Exercise 3.2

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9

Q.1 Evaluate :

i. 8 !

8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 40320

∴ 8! = 40320.

ii. 10 !

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 3628800

iii. 10 ! - 6 !

10! – 6! = 10 × 9 × 8 × 7 × 6! – 6!

= 6!(5040 – 1)

= 6 × 5 × 4 × 3 × 2 × 1 × 5039

= 3628080

∴ 10! – 6! = 3628080

iv. (10 - 6) !

(10 – 6)! = 4!

= 4 × 3 × 2 × 1

= 24

Q.2 Compute :

i. $\frac{12!}{6!}$

$\frac{12!}{6!} = \frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6!}{6!}$

= 12 × 11 × 10 × 9 × 8 × 7

= 665280

ii. $(\frac{12}{6})!$

$(\frac{12}{6})!$ = 2!

= 2 × 1

= 2

iii. (3 × 2) !

(3 × 2)! = 6!

= 6 × 5 × 4 × 3 × 2 × 1

= 720

∴ (3 × 2)! = 720.

iv. 3 ! × 2 !

3! × 2!

= 3 × 2 × 1 × 2 × 1

= 12

v. $\frac{9!}{3! 6!}$

$\frac{9!}{3! 6!} = \frac{9 \times 8 \times 7 \times 6!}{3 \times 2 \times 1 \times 6!}$

= 3 × 4 × 7

= 84

∴ $\frac{9!}{3! 6!}$ = 84.

vi. $\frac{6! - 4!}{4!}$

$\frac{6! - 4!}{4!} = \frac{6 \times 5 \times 4! - 4!}{4!}$

= $\frac{4! (6 \times 5 - 1)}{4!}$

= 29

vii. $\frac{8!}{6! - 4!}$

$\frac{8!}{6! - 4!} = \frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(6 \times 5 \times 4 \times 3 \times 2 \times 1) - (4 \times 3 \times 2 \times 1)}$

= $\frac{40320}{720 - 24}$

= $\frac{40320}{696}$

= $\frac{1680}{29}$

∴ $\frac{8!}{6! - 4!} = \frac{1680}{29}$

= 57.93

viii. $\frac{8!}{(6 - 4)!}$

$\frac{8!}{(6 - 4)!} = \frac{8!}{2!}$

= $\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2!}{2!}$

= 20160

Q.3 Write in terms of factorials :

i. 5 × 6 × 7 × 8 × 9 × 10

5 × 6 × 7 × 8 × 9 × 10

= $\frac{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times 10}{1 \times 2 \times 3 \times 4}$

= $\frac{10!}{4!}$

∴ 5 × 6 × 7 × 8 × 9 × 10 = $\frac{10!}{4!}$

ii. 3 × 6 × 9 × 12 × 15

3 × 6 × 9 × 12 × 15

= 3 × (3 × 2) × (3 × 3) × (3 × 4) × (3 × 5)

= (3⁵) (5 × 4 × 3 × 2 × 1)

= 3⁵ (5!)

iii. 6 × 7 × 8 × 9

6 × 7 × 8 × 9

= $\frac{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9}{1 \times 2 \times 3 \times 4 \times 5}$

= $\frac{9!}{5!}$

∴ 6 × 7 × 8 × 9 = $\frac{9!}{5!}$

iv. 5 × 10 × 15 × 20

5 × 10 × 15 × 20 = (5 × 1) × (5 × 2) × (5 × 3) × (5 × 4)

= (5⁴) (4 × 3 × 2 × 1)

= (5⁴) (4!)

Q.4 Evaluate : $\frac{n!}{r! (n - r)!}$ for

i. n = 8, r = 6

n = 8, r = 6

∴ $\frac{n!}{r! (n - r)!} = \frac{8!}{6! (8 - 6)!}$

= $\frac{8!}{6! \times 2!}$

= $\frac{8 \times 7 \times 6!}{6! \times 2 \times 1}$

= 28.

ii. n = 12, r = 12

n = 12, r = 12

∴ $\frac{n!}{r! (n - r)!} = \frac{12!}{12! (12 - 12)!}$

= $\frac{12!}{12! 0!}$

= 1 ...[∵ 0! = 1]

iii. n = 15, r = 10

n = 15, r = 10

∴ $\frac{n!}{r! (n - r)!} = \frac{15!}{10! (15 - 10)!}$

= $\frac{15!}{10! \times 5!}$

= $\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10!}{10! \times 5 \times 4 \times 3 \times 2 \times 1}$

= 3003.

iv. n = 15, r = 8

n = 15, r = 8

∴ $\frac{n!}{r! (n - r)!} = \frac{15!}{8! (15 - 8)!}$

= $\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8!}{8! \times 7!}$

= $\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9}{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}$

= 5 × 13 × 11 × 9

= 6435

Q.5 Find n, if :

i. $\frac{n}{8!} = \frac{3}{6!} + \frac{1!}{4!}$

$\frac{n}{8!} = \frac{3}{6!} + \frac{1!}{4!}$

∴ $\frac{n}{8!} = \frac{3}{6 \times 5 \times 4!} + \frac{1}{4!}$

∴ $\frac{n}{8 \times 7 \times 6 \times 5 \times 4!} = \frac{1}{4!} [\frac{1}{10} + 1]$

∴ $\frac{n}{8 \times 7 \times 6 \times 5} = \frac{11}{10}$

∴ n = $\frac{8 \times 7 \times 6 \times 5 \times 11}{10}$

∴ n = 1848.

ii. $\frac{n}{6!} = \frac{4}{8!} + \frac{3}{6!}$

$\frac{n}{6!} = \frac{4}{8!} + \frac{3}{6!}$

∴ $\frac{n}{6!} - \frac{3}{6!} = \frac{4}{8!}$

∴ $\frac{n - 3}{6!} = \frac{4}{8 \times 7 \times 6!}$

∴ n – 3 = $\frac{4}{8 \times 7}$

∴ n – 3 = $\frac{1}{14}$

∴ n = $\frac{1}{14} + 3$

= $\frac{43}{14}$

iii. $\frac{1!}{n!} = \frac{1!}{4!} - \frac{4}{5!}$

$\frac{1!}{n!} = \frac{1!}{4!} - \frac{4}{5!}$

∴ $\frac{1!}{n!} = \frac{1!}{4!} - \frac{4}{5 \times 4!}$

∴ $\frac{1!}{n!} = \frac{1!}{4!} [1 - \frac{4}{5}]$

∴ $\frac{1}{n!} = \frac{1}{4!} \times \frac{1}{5} = \frac{1}{5!}$

∴ n! = 5!

∴ n = 5.

iv. (n + 1)! = 42 × (n – 1) !

(n + 1)! = 42 × (n – 1)!

∴ (n + 1) n (n – 1)! = 42(n – 1)!

∴ n² + n = 42

∴ n² + n – 42 = 0

∴ (n + 7)(n – 6) = 0

∴ n = – 7 or n = 6

But n ≠ – 7 as n ∈ N

∴ n = 6

v. (n + 3)! = 110 × (n + 1) !

(n + 3)! = 110 × (n + 1)!

(n + 3)(n + 2)(n + 1)! = 110(n + 1)!

∴ (n + 3)(n + 2) = 110

∴ n² + 5n + 6 = 110

∴ n² + 5n + 6 – 110 = 0

∴ n² + 5n – 104 = 0

∴ n² + 13n – 8n – 104 = 0

∴ n(n + 3) – 8(n + 13) = 0

∴ (n + 13)(n – 8) = 0

∴ n + 13 = 0 or n – 8 = 0

∴ n = – 13 or n = 8

But n ∈ N

∴ n ≠ – 13

Hence, n = 8.

Q.6 Find n, if :

i. $\frac{(17 - n)!}{(14 - n)!}$ = 5 !

$\frac{(17 - n)!}{(14 - n)!}$ = 5!

∴ $\frac{(17 - n) (16 - n) (15 - n) (14 - n)!}{(14 - n)!}$

= 5 × 4 × 3 × 2 × 1

∴ (17 – n) (16 – n) (15 – n) = 6 × 5 × 4

Comparing on both sides, we get

17 – n = 6

∴ n = 11

ii. $\frac{(15 - n)!}{(13 - n)!}$ = 12

$\frac{(15 - n)!}{(13 - n)!}$ = 12

∴ $\frac{(15 - n) (14 - n) (13 - n)!}{(13 - n)!}$ = 12

∴ (15 – n)(14 – n) = 12 = 4 × 3

∴ (15 – n)(14 – n) = (15 – 11)(14 – 11)

∴ n = 11.

iii. $\frac{n!}{3! (n - 3)!} : \frac{n!}{5! (n - 5)!}$ = 5 : 3

$\frac{n!}{3! (n - 3)!} : \frac{n!}{5! (n - 5)!}$ = 5 : 3

∴ $\frac{n!}{3! (n - 3)!} \times \frac{5! (n - 5)!}{n!} = \frac{5}{3}$

∴ $\frac{n!}{3! (n - 3) (n - 4) (n - 5)!} \times \frac{5 \times 4 \times 3! (n - 5)!}{n!} = \frac{5}{3}$

∴ $\frac{5 \times 4}{(n - 3) (n - 4)} = \frac{5}{3}$

∴ 12 = (n – 3)(n – 4)

∴ (n – 3)(n – 4) = 4 × 3

Comparing on both sides, we get

n – 3 = 4

∴ n = 7

iv. $\frac{n!}{3! (n - 3)!} : \frac{n!}{5! (n - 7)!}$ = 1 : 6

$\frac{n!}{3! (n - 3)!} : \frac{n!}{5! (n - 7)!}$ = 1 : 6

∴ $\frac{n!}{3! (n - 3)!} \times \frac{5! (n - 7)!}{n!} = \frac{1}{6}$

∴ $\frac{5! (n - 7)!}{3! (n - 3)!} = \frac{1}{6}$

∴ $\frac{5 \times 4 \times 3! \times (n - 7)!}{3! \times (n - 3) (n - 4) (n - 5) (n - 6) (n - 7)!} = \frac{1}{6}$

∴ $\frac{5 \times 4}{(n - 3) (n - 4) (n - 5) (n - 6)} = \frac{1}{6}$

∴ (n – 3)(n – 4)(n – 5)(n – 6) = 6 × 5 × 4

∴ (n – 3)(n – 4)(n – 5)(n – 6) = 5 × 4 × 3 × 2

∴ (n – 3)(n – 4)(n – 5)(n – 6) = (8 – 3)(8 – 4)(8 – 5)(8 – 6)

∴ n = 8

v. $\frac{(2 n)!}{7! (2 n - 7)!} : \frac{n!}{4! (n - 4)!}$ = 24 : 7

$\frac{(2 n)!}{7! (2 n - 7)!} : \frac{n!}{4! (n - 4)!}$ = 24 : 1

∴ $\frac{(2 n)!}{7! (2 n - 7)!} \times \frac{4! (n - 4)!}{n!}$ = 24

∴ $\frac{(2 n) (2 n - 1) (2 n - 2) (2 n - 3) (2 n - 4) (2 n - 5) (2 n - 6) (2 n - 7)!}{7 \times 6 \times 5 \times 4! (2 n - 7)!} \times \frac{4! (n - 4)!}{n (n - 1) (n - 2) (n - 3) (n - 4)!}$ = 24

∴ $\frac{(2 n) (2 n - 1) (2 n - 2) (2 n - 3) (2 n - 4) (2 n - 5) (2 n - 6)}{7 \times 6 \times 5} \times \frac{1}{n (n - 1) (n - 2) (n - 3)}$ = 24

∴ $\frac{(2 n) (2 n - 1) 2 (n - 1) (2 n - 3) 2 (n - 2) (2 n - 5) 2 (n - 3)}{7 \times 6 \times 5} \times \frac{1}{n (n - 1) (n - 2) (n - 3)}$ = 24

∴ $\frac{16 (2 n - 1) (2 n - 3) (2 n - 5)}{7 \times 6 \times 5}$ = 24

∴ (2n – 1) (2n – 3) (2n – 5) = $\frac{24 \times 7 \times 6 \times 5}{16}$

∴ (2n – 1) (2n – 3) (2n – 5) = 9 × 7 × 5

Comparing on both sides, we get

∴ 2n – 1 = 9

∴ n = 5

Q.7 Show that : $\frac{n!}{r! (n - r)!} + \frac{n!}{(r - 1)! (n - r + 1)!}$

$= \frac{(n + 1)!}{r! (n - r + 1)!}$

L.H.S. = $\frac{n!}{r! (n - r)!} + \frac{n!}{(r - 1)! (n - r + 1)!}$

= $n! [\frac{1}{r (r - 1)! (n - r)!} + \frac{1}{(r - 1)! (n - r + 1) (n - r)!}]$

= $\frac{n!}{(r - 1)! (n - r)!} [\frac{1}{r} + \frac{1}{n - r + 1}]$

= $\frac{n!}{(r - 1)! (n - r)!} [\frac{n - r + 1 + r}{r (n - r + 1)}]$

= $\frac{n!}{(r - 1)! (n - r)!} [\frac{n + 1}{r (n - r + 1)}]$

= $\frac{(n + 1) n!}{[r (r - 1)!] [(n - r + 1) (n - r)!]}$

= $\frac{(n + 1)!}{r! (n - r + 1)!}$

= R.H.S.

Hence, $\frac{n!}{r! (n - r)!} + \frac{n!}{(r - 1)! (n - r + 1)!} = \frac{(n + 1)!}{r! (n - r + 1)!}$

Q.8 Show that : $\frac{9!}{3! 6!} + \frac{9!}{4! 5!} = \frac{10!}{4! 6!}$

L.H.S. = $\frac{9!}{3! 6!} + \frac{9!}{4! 5!}$

= $\frac{9!}{3! \times 6 \times 5!} + \frac{9!}{4 \times 3! \times 5!}$

= $\frac{9!}{3! 5!} [\frac{1}{6} + \frac{1}{4}]$

= $\frac{9!}{3! 5!} [\frac{4 + 6}{6 \times 4}]$

= $\frac{10 \times 9!}{6 \times 5! \times 4 \times 3!}$

= $\frac{10!}{6! 4!}$

= $\frac{10!}{4! 6!}$

= R.H.S.

Q.9 Show that : $\frac{(2 n)!}{n!}$ = 2ⁿ (2n – 1)(2n – 3) ... 5 . 3 . 1

L.H.S. = $\frac{(2 n)!}{n!}$

= $\frac{2 n (2 n - 1) (2 n - 2) (2 n - 3) (2 n - 4) ... 5.4 .3 .2 .1}{n!}$

= $\frac{[2 n (2 n - 2) (2 n - 4) ... 6.4 .2] [(2 n - 1) (2 n - 3) ... 5.3 .1]}{n!}$

= $\frac{[2 (n) \cdot 2 (n - 1) \cdot 2 (n - 2) ... 2 (3) \cdot 2 (2) \cdot 2 (1)] \cdot [(2 n - 1) (2 n - 3) ... 5.3 .1]}{n!}$

= $\frac{[2^{n} (n) (n - 1) (n - 2) ... 3.2 .1] [(2 n - 1) (2 n - 3) ... 5.3 .1]}{n!}$

= $\frac{2^{n} \times n! [(2 n - 1) (2 n - 3) ... 5.3 .1]}{n!}$

= 2ⁿ(2n – 1)(2n – 3) ... 5.3.1

= R.H.S.

Q.10 Simplyfy :

i. $\frac{(2 n + 2)!}{(2 n)!}$

$\frac{(2 n + 2)!}{(2 n)!} = \frac{(2 n + 2) (2 n + 1) (2 n)!}{(2 n)!}$

= 2(n + 1) (2n + 1)

ii. $\frac{(n + 3)!}{(n^{2} - 4) (n + 1)!}$

$\frac{(n + 3)!}{(n^{2} - 4) (n + 1)!} = \frac{(n + 3) (n + 2) (n + 1)!}{(n^{2} - 4) (n + 1)!}$

= $\frac{(n + 3) (n + 2)}{n^{2} - 4}$

= $\frac{(n + 3) (n + 2)}{(n - 2) (n + 2)}$

= $\frac{n + 3}{n - 2}$ .

iii. $\frac{1}{n!} - \frac{1}{(n - 1)!} - \frac{1}{(n - 2)!}$

$\frac{1}{n!} - \frac{1}{(n - 1)!} - \frac{1}{(n - 2)!}$

= $\frac{1}{n (n - 1) (n - 2)!} - \frac{1}{(n - 1) (n - 2)!} - \frac{1}{(n - 2)!}$

= $\frac{1}{(n - 2)!} [\frac{1}{n (n - 1)} - \frac{1}{(n - 1)} - 1]$

= $\frac{1}{(n - 2)!} [\frac{1 - n - n (n - 1)}{n (n - 1)}]$

= $\frac{1 - n^{2}}{n (n - 1) (n - 2)!}$

= $\frac{- (n - 1) (n + 1)}{n (n - 1) (n - 2)!}$

= $\frac{- (n + 1)}{n (n - 2)!}$

iv. Simplify n[n! + (n – 1)!] + n²(n – 1)! + (n + 1)!

n[n! + (n – 1)!] + n²(n – 1)! + (n + 1)!

= n[n(n – 1)! + (n – 1)!] + n²(n – 1)! + (n + 1)n(n – 1)!

= (n – 1)! [n(n + 1) + n² + (n + 1)n]

= (n – 1)! [n² + n + n² + n² + n]

= (n – 1)! (3n² + 2n)

= n(n – 1)! (3n + 2) = (3n + 2)n!

v. $\frac{n + 2}{n!} - \frac{3 n + 1}{(n + 1)!}$

$\frac{n + 2}{n!} - \frac{3 n + 1}{(n + 1)!} = \frac{n + 2}{n!} - \frac{3 n + 1}{(n + 1) . n!}$

= $\frac{(n + 1) (n + 2) - (3 n + 1)}{(n + 1) \cdot n!}$

= $\frac{n^{2} + 3 n + 2 - 3 n - 1}{(n + 1) \cdot n!}$

= $\frac{n^{2} + 1}{(n + 1)!}$

vi. $\frac{1}{(n - 1)!} + \frac{1 - n}{(n + 1)!}$

$\frac{1}{(n - 1)!} + \frac{1 - n}{(n + 1)!}$

= $\frac{1}{(n - 1)!} [\frac{n (n + 1) + (1 - n)}{n (n + 1)}]$

= $\frac{1}{(n - 1)!} [1 + \frac{1 - n}{n (n + 1)}]$

= $\frac{1}{(n - 1)!} [\frac{n (n + 1) + (1 - n)}{n (n + 1)}]$

= $\frac{1}{(n - 1)!} [\frac{n^{2} + n + 1 - n}{n (n + 1)}]$

= $\frac{n^{2} + 1}{n (n - 1)! (n + 1)}$

= $\frac{n^{2} + 1}{n! \times (n + 1)}$

= $\frac{n^{2} + 1}{(n + 1)!}$

vii. $\frac{1}{n!} - \frac{3}{(n + 1)!} - \frac{n^{2} - 4}{(n + 2)!}$

$\frac{1}{n!} - \frac{3}{(n + 1)!} - \frac{n^{2} - 4}{(n + 2)!}$

= $\frac{1}{n!} - \frac{3}{(n + 1) n!} - \frac{(n - 2) (n + 2)}{(n + 2) (n + 1) n!}$

= $\frac{1}{n!} [1 - \frac{3}{n + 1} - \frac{n - 2}{n + 1}]$

= $\frac{1}{n!} [\frac{n + 1 - 3 - n + 2}{n + 1}]$

= $\frac{1}{n!} \times 0$

= 0

viii. $\frac{n^{2} - 9}{(n + 3)!} + \frac{6}{(n + 2)!} - \frac{1}{(n + 1)!}$

$\frac{n^{2} - 9}{(n + 3)!} + \frac{6}{(n + 2)!} - \frac{1}{(n + 1)!}$

= $\frac{(n - 3) (n + 3)}{(n + 3) (n + 2) (n + 1)!} + \frac{6}{(n + 2) (n + 1)!} - \frac{1}{(n + 1)!}$

= $\frac{1}{(n + 1)!} [\frac{n - 3 + 6 - n - 2}{n + 2}]$

= $\frac{1}{(n + 1)!} [\frac{n - 3}{n + 2} + \frac{6}{n + 2} - 1]$

= $\frac{1}{(n + 1)!} [\frac{n - 3 + 6 - n - 2}{n + 2}]$

= $\frac{1}{(n + 2)!}$

Exercise 3.3

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9 Q.10 Q.11 Q.12 Q.13 Q.14 Q.15 Q.16 Q.17

Q.1 Find n, if ⁿP₆ : ⁿP₃ = 120 : 1

ⁿP₆ : ⁿP₃ = 120 : 1

∴ $\frac{n!}{(n - 6)!} \times \frac{(n - 3)!}{n!}$

∴ $\frac{n!}{(n - 6)!} \times \frac{(n - 3)!}{n!}$ = 120

∴ $\frac{n!}{(n - 6)!} \times \frac{(n - 3) (n - 4) (n - 5) (n - 6)!}{n!}$

∴ (n – 3) (n – 4) (n – 5) = 120

∴ (n – 3) (n – 4) (n – 5) = 6 × 5 × 4

Comparing on both sides, we get

n – 3 = 6

∴ n = 9

Q.2 Find m and n, if ^(m+n)P₂ = 56 and ^(m-n)P₂ = 12

^(m+n)P₂ = 56

∴ $\frac{(m + n)!}{(m + n - 2)!}$ = 56

∴ (m + n)(m + n – 1) = 56

∴ (m + n)² – (m + n) – 56 = 0

Let a = m + n

∴ a² – a – 56 = 0

∴ a² – 8a + 7a – 56 = 0

∴ a(a – 8) + 7(a – 8) = 0

∴ (a – 8)(a + 7) = 0

∴ a – 8 = 0 or a + 7 = 0

∴ a = 8 or a = – 7

∴ m + n = 8 or m + n = – 7

But m + n > 0

∴ m + n = 8 ...(1)

^(m-n)P₂ = 12

∴ $\frac{(m - n)!}{(m - n - 2)!}$ = 12

∴ (m – n)(m – n – 1) = 12

∴ (m – n)² – (m – n) = 12

Let b = m – n

∴ b² – b – 12 = 0

∴ b² – 4b + 3b – 12 = 0

∴ b(b – 4) + 3(b – 4) = 0

∴ (b – 4)(b + 3) = 0

∴ b – 4 = 0 or b + 3 = 0

∴ b = 4 or b = – 3

∴ m – n = 4 or m – n = – 3

But m – n > 0

∴ m – n = 4 ...(2)

Adding equations (1) and (2), we get,

m + n = 8
m – n = 4
∴ 2m = 12

∴ m = 6

Putting m = 6 in equation (1), we get,

6 + n = 8

∴ n = 8 – 6

∴ n = 2

Hence, m = 6, n = 2

Q.3 Find r, if ¹²P_r–2 : ¹¹P_r–1 = 3 : 14

¹²P_r–2 : ¹¹P_r–1 = 3 : 14

∴ $\frac{12!}{(12 - r + 2)!} \div \frac{11!}{(11 - r + 1)!} = \frac{3}{14}$

∴ $\frac{12!}{(14 - r)!} \times \frac{(12 - r)!}{11!} = \frac{3}{14}$

∴ $\frac{12 \times 11!}{(14 - r) (13 - r) (12 - r)!} \times \frac{(12 - r)!}{11!} = \frac{3}{14}$

∴ $\frac{12}{(14 - r) (13 - r)} = \frac{3}{14}$

∴ (14 – r)(13 – r) = 8 × 7

Comparing on both sides, we get

∴ 14 – r = 8

∴ r = 6

Q.4 Show that (n + 1) (ⁿP_r) = (n – r + 1) [⁽ⁿ⁺¹⁾P_r]

L.H.S. = (n + 1) (ⁿP_r)

= $(n + 1) \frac{n!}{(n - r)!}$

= $\frac{(n + 1)!}{(n - r)!}$ ...(1)

R.H.S. = (n – r + 1) [⁽ⁿ⁺¹⁾P_r]

= $(n - r + 1) \cdot \frac{(n + 1)!}{(n + 1 - r)!}$

= $(n - r + 1) \cdot \frac{(n + 1)!}{(n - r + 1)!}$

= $(n - r + 1) \cdot \frac{(n + 1)!}{(n - r + 1) (n - r)!}$

= $\frac{(n + 1)!}{(n - r)!}$ ...(2)

From (1) and (2), we get, L.H.S. = R.H.S.

Hence, (n + 1) (ⁿP_r) = (n – r + 1) [⁽ⁿ⁺¹⁾P_r]

Q.5 How many 4 letter words can be formed using letters in the word MADHURI, if :

i. letters can be repeated :

There are 7 letters in the word MADHURI.

A 4 letter word is to be formed from the letters of the word MADHURI and repetition of letters is allowed.

1^st letter can be filled in 7 ways.

2^nd letter can be filled in 7 ways.

3^rd letter can be filled in 7 ways.

4^th letter can be filled in 7 ways.

∴ Total no. of ways a 4-letter word can be formed

= 7 x 7 x 7 x 7

= 2401

∴ 2401 four-lettered words can be formed when repetition of letters is allowed.

ii. letters cannot be repeated :

There are 7 different letters in the word 'MADHURI' and we have to form 4-letter words.

i.e., n = 7 and r = 4

If the repetition of letters is not allowed, then the number of 4-letter words

ⁿP_r = ⁷P₄

= $\frac{7!}{(7 - 4)!}$

= $\frac{7!}{3!}$

= $\frac{7 \times 6 \times 5 \times 4 \times 3!}{3!}$

= 840.

Q.6 Determine the number of arrangements of letters of the word ALGORITHM if :

i. vowels are always together :

There are 9 letters in the word ALGORITHM.

When vowels are always together.

There are 3 vowels in the word ALGORITHM (i.e. A, I, O).

Let us consider these 3 vowels as one unit.

This unit with 6 other letters is to be arranged.

∴ The number of arrangement = ⁷P₇ i.e., 7!

3 vowels can be arranged among themselves in ³P₃ i.e., 3! ways.

∴ Required number of arrangements

= 7! × 3!

= 5040 × 6

= 30240

∴ 30240 words can be formed if vowels are always together.

ii. no two vowels are together :

In the word 'ALGORITHM' the number of letters is n = 9.

No two vowels are together:

Consider one of the possible arrangements of V (vowels) and C (consonants)

VCVCVCVCVCVCV

Here, there are 7 positions for vowels and 6 positions for consonants.

∴ 3 vowels can be arranged in ⁷P₃ ways and 6 consonants can be arranged in ⁶P₆ ways.

Hence, the total number of words in which no two vowels are together

= ⁷P₃ × ⁶P₆

= $\frac{7!}{4!} \times 6!$

= 7 × 6 × 5 × (6 × 5 × 4 × 3 × 2 × 1)

= 210 × 720

= 151200

iii. consonants are at even position :

In the word ALGORITHM even positions are 4 and consonants are 6.

∴ number of arrangements in which 6 consonants occupy 4 even positions = ⁶P₄

Now, the remaining 5 positions can be occupied by remaining 5 letters in ⁵P₅ ways.

Hence, the total number of words in which consonants occupy even positions

= $\frac{6!}{(6 - 4)!} \times 5! ... [\begin{matrix} ^{n} P_{r} = \frac{n!}{(n - r)!} \\ ^{n} P_{r} = n! \end{matrix}]$

= $\frac{6 \times 5 \times 4 \times 3 \times 2!}{2!} \times 5!$

= 6 × 5 × 4 × 3 × (5 × 4 × 3 × 2 × 1)

= 360 × 120

= 43200

∴ 43200 words can be formed if the consonants are at even positions.

iv. O is the first and T is the last letter :

In the word 'ALGORITHM' the number of letters is n = 9.

O is the first and T is the last letter:

Here, two positions for 'O' and 'T' are fixed and the remaining 7 positions are left for the remaining 7 letters.

Hence, the total number of words in which they begin with 'O' and end with 'T' = ⁷P₇ = 7!

= 7 × 6 × 5 × 4 × 3 × 2 × 1

= 5040

Q.7 In a group photograph, 6 teachers and principal are in the first row and 18 students are in the second row. There are 12 boys and 6 girls among the students. If the middle position is reserved for the principal and if no two girls are together, find the number of arrangements.

In the 1^st row, 6 teachers can be arranged among themselves in ⁶P₆ i.e., 6! ways.

In the 2^nd row, 12 boys can be arranged among themselves in ¹²P₁₂ i.e., 12! ways.

So, there are 13 places group created by 12 boys in which 6 girls occupy any 6 places in ¹³P₆ ways.

∴ Required number of arrangements

= 6! × 12! × ¹³P₆

= $6! \times 12! \times \frac{13!}{(13 - 6)!}$

= $\frac{6! \times 12! \times 13!}{7 \times 6!}$

= $6! \times 12! \times \frac{13!}{7!}$

= $\frac{12! 13!}{7}$

Q.8 Find the numbers of ways so that letters of the word HISTORY can be arranged as, :

i. Y and T are together :

In the word 'HISTORY', the number of letters is n = 7.

Words in which Y and T are together:

Since Y and T are always together, consider them as a single unit.

Now we have 1 + 5 = 6 different letters, that can be arranged in ⁶P₆ ways.

After this is done Y and T can be arranged amongst themselves in ²P₂ ways.

Hence, the total number of words formed in which Y and T are together is given by

⁶P₆ × ²P₂ = 6! × 2!

= 6 × 5 × 4 × 3 × 2 × 1 × 2 × 1

= 720 × 2

= 1440

ii. Y is next to T :

There are 7 letters in the word HISTORY

When ‘Y’ is next to ‘T’

Let us take this (‘Y’ next to ‘T’) as one unit.

This unit with 5 other letters is to be arranged.

∴ The number of arrangments of 6 letters and one unit = ⁶P₆ = 6!

Also ‘Y’ has to be always next to ‘T’.

So they can be arranged in 1 way.

∴ total number of arrangements possible when Y is next to T

= 6! × 1

= 720

∴ 720 words can be formed if Y is next to T.

iii. there is no restriction :

In the word 'HISTORY', the number of letters is n = 7.

Words in which there is no restriction:

When there is no restriction, the 7 letters of the word 'HISTORY' can be arranged amongst themselves in ⁷P₇ ways.

Hence, the total number of words when there is no restriction

= ⁷P₇ = 7!

iv. begin and end with vowel :

There are 7 letters in the word HISTORY

When begin and end with vowel

there are 2 vowels in the word HISTORY

All other letters of the word HISTORY are to be arranged between 2 vowels such that arrangement begins and ends with vowel.

Other 5 letters can be filled between the two vowels in ⁵P₅ i.e., 5! Ways

Also, 2 vowels can be arranged among themselves in ²P₂ i.e., 2! Ways

∴ total number of arrangements when the word begins and ends with vowel

= 5! × 2!

= 120 × 2

= 240

∴ 240 words can be formed if the arrangement begins and ends with vowel.

v. end in ST :

In the word 'HISTORY', the number of letters is n = 7.

Words end in ST:

Since the words end in ST, therefore we have to arrange only 5 positions from the remaining 5 letters.

This can be done in ⁵P₅ ways.

Hence, the total number of words end in ST

= ⁵P₅

= 5!

= 5 × 4 × 3 × 2 × 1

= 120

vi. begin with S and end with T :

When word begins with S and ends with T.

As arrangenent begins with S and ends with T,

remaining 5 letters can be arranged between S and T among themselves in ⁵P₅ = 5! = 120 ways.

∴ Total number of arrangments when the word begins with S and ends with T.

= 120

Q.9 Find the number of arrangments of the letters in the word SOLAPUR so that consonants and vowels are placed alternately.

In the word 'SOLAPUR', the number of letters is n = 7.

Vowels are O, A, U, and consonants are S, L, P, R

Since consonants and vowels are placed alternately, the four consonants must occur at 4 odd places and three vowels must occur at 3 even places.

Now, 4 consonants can be arranged in ⁴P₄ ways and 3 vowels can be arranged in ³P₃ ways.

Hence, the number of arrangements in which consonants and vowels are placed alternately

= ⁴P₄ × ³P₃

= 4!3!

= 4 × 3 × 2 × 1 × 3 × 2 × 1

= 144

Q.10 Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6, 8 if :

i. digits can be repeated :

A 4 digit number is to be made from the digits 1, 2, 4, 5, 6, 8 such that digits can be repeated.

∴ Unit’s place digit can be filled in 6 ways.

10’s place digit can be filled in 6 ways.

100’s place digit can be filled in 6 ways.

1000’s place digit can be filled in 6 ways.

∴ total number of numbers

= 6 × 6 × 6 × 6

= 6⁴

= 1296

∴ 1296 four-digit numbers can be formed if repetition of digits is allowed.

ii. digits cannot be repeated :

There are 6 different digits and we have to form 4-digit numbers, i.e., n = 6, r = 4.

If the repetition of digits is not allowed, then the number of 4-digit numbers

= ⁶P₄

= $\frac{6!}{2!}$

= $\frac{6 \times 5 \times 4 \times 3 \times 2!}{2!}$

= 360.

Q.11 How many numbers can be formed using the digits 0, 1, 2, 3, 4, 5 without repetition so that resulting numbets are between 100 and 1000 ?

A number between 100 and 1000 that can be formed from the digits 0, 1, 2, 3, 4, 5 is of 3 digits and repetition of digits is not allowed.

∴ 100’s place can be filled in 5 ways as it is a non-zero number which

10’s place digits can be filled in 5 ways.

Unit’s place digit can be filled in 4 ways.

∴ total number of ways the number can be formed

= 5 × 5 × 4

= 100

∴ 100 numbers between 100 and 1000 can be formed.

Q.12 Find the number of 6-digit numbers using the digits 3, 4, 5, 6, 7, 8 without repetition. How many of these numbers are :

i. divisible by 5 :

There are 6 different digits and we have to form 6-digit numbers, i.e., n = 6, r = 6

If no digit is repeated, the total numbers with 6-digits can be formed = ⁿP_r

= ⁶P₆

= 6!

= 6 x 5 x 4 x 3 x 2 x 1

= 720.

Since the number is divisible by 5, the unit's place of 6-digits number can be filled in only one way by the digit 5.

Remaining 5 positions can be filled from the remaining 5 digits in ⁵P₅ ways.

Hence, the total number of 6-digit numbers divisible by 5 = 1 x ⁵P₅ = 5!

= 5 x 4 x 3 x 2 x 1

= 120.

ii. not divisible by 5 :

A number of 6 different digits is to be formed from the digits 3, 4, 5, 6, 7, 8 which can be done in ⁶P₆ i.e., 6! = 720 ways

If the number is not divisible by 5

Unit’s place can be any digit from 3, 4, 6, 7, 8 which can be selected in 5 ways.

Other 5 digits can be arranged in ⁵P₅

i.e., 5! ways

∴ Required number of numbers not divisible by 5

= 5 × 5!

= 5 × 120

= 600

Q.13 A code word is formed by two different English letters followed by two non-zero distinct digits. Find the number of such code words. Also, find the number of such code words that end with an even digit.

There are 26 alphabets and 9 non-zero digits from 1 to 9.

For a code, 2 distinct alphabets can be arranged in ²⁶P₂ ways and 2 digits can be arranged in ⁹P₂ ways.

Hence, the total number of codewords available

= $\frac{26!}{24!} \times \frac{9!}{7!}$

= $\frac{26 \times 25 \times 24!}{24!} \times \frac{9 \times 8 \times 7!}{7!}$

= (26 × 25) × (9 × 8)

= 650 × 72

= 46800

For a code, 2 alphabets can be arranged in ²⁶P₂ ways, and of the, 2 distinct digits the last place can be filled by either 2, 4, 6, 8, i.e., 4 ways, while the first place of the digit can be filled from the remaining 8 digits in 8 ways.

Hence, the total number of code words that end with an even integer

= ²⁶P₂ × 4 × 8

= 26 × 25 × 4 × 8

= 20800

Q.14 Find the number of ways in which 5 letters can be posted in 3 post boxes if any number of letters can be posted in a post box.

There are 5 letters and 3 post boxes and any number of letters can be posted in all of three post boxes.

∴ Each letter can be posted in 3 ways.

∴ Total number of ways 5 letters can be posted

= 3 × 3 × 3 × 3 × 3

= 243

Q.15 Find the number of arranging 11 distinct objects taken 4 at a time so that a specified object :

i. always occurs :

Here n = 11, r = 4

One particular thing always occur:

The number of permutations = r × ^n–1P_r–1

Putting r = 4, n = 11, we get the number of permutations

= $4 \times^{(11 - 1)} P_{(4 - 1)}$

= 4 × ¹⁰P₃

= $4 \times \frac{10!}{7!}$

= 4 × 10 × 9 × 8

= 2880

ii. never occurs :

There are 11 distinct objects and 4 are to be taken at a time.

When one particular object will not occur then 4 object are to be arranged from 10 objects which can be done in ¹⁰P₄ ways

= 10 × 9 × 8 × 7

= 5040

∴ In 5040 permutations of 11 distinct objects, taken 4 at a time, one particular object will never occur.

Q.16 In how many ways can 5 different books be arranged on a shelf if :

i. there are no restrictions :

When there are no restrictions, the 5 books can be arranged in ⁵P₅ ways.

Hence, the required number of arrangements

= ⁵P₅

= 5!

= 5 × 4 × 3 × 2 × 1

= 120

ii. 2 books are always together :

2 books are together

Say books are B₁, B₂, B₃, B₄, B₅ are to be arranged with B₁, B₂ together.

Required number = 2 × 4! = 48

iii. 2 books are never together :

Since 2 books are never together, we can arrange these two books at 4 places (2 places in between the remaining 3 books + 2 at the ends) in ⁴P₂ ways.

After this the remaining 3 books can be arranged in ³P₃ ways.

Hence, the total number of arrangements in which 2 books are never together

= ⁴P₂ × ³P₃

= $\frac{4!}{2!} \times 3!$

= $\frac{4 \times 3 \times 2 \times 1}{2!} \times 3 \times 2!$

= 72.

Q.17 3 boys and 3 girls are to sit in a row. How many ways can this be done if :

i. there are no restrictions :

As there is no restriction

Required number = 6! = 720

ii. there are no restrictions :

The two ends can be occupied by 3 girls in ³P₂ ways.

After this the remaining 4 persons can sit at remaining 4 places in ⁴P₄ ways.

Hence, the total number of seating arrangements

= ³P₂× ⁴P₄

= $\frac{3!}{1!} \times 4!$

= 3 × 2 × 1 × 4 × 3 × 2 × 1

= 144.

iii. boys and girls are at alternate places :

B _ B _ B _ or G _ G _ G _
↑ ↑ ↑ ↑ ↑ ↑
G G G B B B

Required number = 2 × 3! × 3! = 72

iv. all boys sit together :

Three boys can sit together in ³P₃ ways. Now considering 3 boys as 1 group, 3 girls and 1 group of boys, i.e., altogether 4 can sit in ⁴P₄ ways.

Hence, the total number of seating arrangements in which all boys sit together

= ³P₃ × ⁴P₄

= 3!4!

= 3 × 2 × 1 × 4 × 3 × 2 × 1

= 144.

Exercise 3.4

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9 Q.10 Q.11 Q.12 Q.13 Q.14 Q.15

Q.1 Find the number of premutations of letters in each of the following words.

i. DIVYA

There are 5 letters in the word DIVYA which can be arranged themselves in 5! ways

= 120 ways

ii. SHANTARAM

In the word 'SHANTARAM', the number of letters is n = 9 of which A repeats thrice, i.e., p = 3 and rest are distinct.

∴ the number of distinct permutations of the letters

= $\frac{n!}{p!}$

= $\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3!}{3!}$

= 9 × 8 × 7 × 6 × 5 × 4

= 60480.

iii. REPRESENT

There are 9 letters in the word REPRESENT in which ‘E’ is repeated 3 times and ‘R’ is repeated 2 times.

∴ Number of permutations of the letters of the word REPRESENT,

= $\frac{9!}{3! 2!}$

= $\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4}{2}$

= 30240

iv. COMBINE

In the word 'COMBINE', the number of letters is n = 7, which are all distinct.

∴ the number of permutations of the letters

= ⁿP_n

= ⁷P₇

= 7!

= 7 × 6 × 5 × 4 × 3 × 2 × 1

= 5040.

v. BALBHARATI

There are 10 letters in the word BALBHARATI in which ‘B’ is repeated 2 times and ‘A’ is repeated 3 times.

∴ Number of permutations of the letters of the word BALBHARATI,

= $\frac{10!}{2! 3!}$

= $\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 3 \times 2}$

= 302400.

Q.2 You have 2 identical books on English, 3 identical books on Hindi and 4 identical books on Mathematics. Find the number of distinct ways of arranging them on a shelf.

2 identical books on English, i.e., p = 2

3 identical books on Hindi, i.e., q = 3

4 identical books on Mathematics, i.e., r = 4

Total number of books is n = 2 + 3 + 4 = 9

∴ the number of distinct ways of arrangement of books on a shelf is

$\frac{n!}{p! q! r!}$

= $\frac{9!}{2! 3! 4!}$

$\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4!}{3 \times 2 \times 1 \times 2 \times 1 \times 4!}$

= 9 × 4 × 7 × 5

= 1260

Q.3 A coin is tossed 8 times. In how many ways can we obtain :

i. 4 heads and 4 tails :

A coin is tossed 8 times. All heads are identical and all tails are identical.

We can obtain 4 heads and 4 tails in $\frac{8!}{4! 4!}$

= $\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2}$

= 70 ways

∴ In 70 different ways we can obtain 4 heads and 4 tails.

ii. at least 6 heads :

A coin is tossed 8 times.

So the number of possible trials is n = 8.

Outcomes are head or tail.

At least 6 heads mean either 6 heads and 2 tails or 7 heads and 1 tail or 8 heads and 0 tail,

i.e., p = 6, q = 2 or p = 7, q = 1 or p = 8, q = 0

∴ the number of ways in which we can obtain at least 6 heads is

$\frac{n!}{p! q!} + \frac{n!}{p! q!} + \frac{n!}{p! q!}$

= $\frac{8!}{6! 2!} + \frac{8!}{7! 1!} + \frac{8!}{8! 0!}$

= $\frac{8 \times 7 \times 6!}{6! \times 2 \times 1} + \frac{8 \times 7!}{7! \times 1} + \frac{8!}{8! \times 1}$

= 28 + 8 + 1

= 37

Q.4 A bag has 5 red, 4 blue and 4 green marbles. If all are drawn one by one and their colours are recorded, how many diffierent arrangements can be found?

There are total 13 marbles in a bag.

Out of these 5 are Red, 4 Blue and 4 are Green marbles.

All balls of same colour are taken to be identical.

∴ Required number of arrangements = $\frac{13!}{5! 4! 4!}$

Q.5 Find the number of ways of arranging letters of the word MATHEMATICAL. How many of these arrangements have all vowels together?

There are 12 letters in the word MATHEMATICAL in which ‘M’ repeats 2 times, ‘A’ repeats 3 times and ‘T’ repeats 2 times.

∴ Total number of arrangements = $\frac{12!}{2! 3! 2!}$

When all the vowels i.e., ‘A’, ‘A’, ‘A’, ‘E’, ‘I’ are to be kept together.

Number of arrangements of these vowels = $\frac{5!}{3!}$ ways.

Let us consider these vowels together as one unit.

This unit is to be arranged with 7 other letters in which ‘M’ and ‘T’ repeated 2 times each.

∴ Number of arrangements = $\frac{8!}{2! 2!}$

∴ Total number of arrangements = $\frac{8! \times 5!}{2! 2! 3!}$

Q.6 Find the number of different arrangements of letters in the word MAHARASHTRA. How many of these arrangements have :

i. letters R and H never together ?

In the word 'MAHARASHTRA' the number of letters is n = 11 of which A repeats 4 times, i.e., p = 4, H repeats twice i.e., q = 2, R repeats twice, i.e., r = 2 and rest are distinct.

∴ the number of different arrangements with the letters of the word MAHARASHTRA is

$\frac{n!}{p! q! r!}$

= $\frac{11!}{4! 2! 2!}$

= $\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4!}{4! \times 2 \times 1 \times 2 \times 1}$

= 11 × 10 × 9 × 2 × 7 × 6 × 5

= 415800

When two R and two H are together forms one unit (object) and taking remaining 7 letters, we have total number of letters is n = 8 of which A repeats 4 times, i.e., p = 4.

Now both R and both H can be arranged together in $\frac{4!}{2! 2!}$

∴ the total number of possible arrangements of letters in which both R and both H are together

= $\frac{8!}{4!} \times \frac{4!}{2! 2!}$

= $\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1}$

= 8 × 7 × 6 × 5 × 3 × 2

= 10080

Hence, the number of arrangements of the letters in which R and H are never together = (Total number of arrangements) − (The number of arrangements in which R and H are together)

= 415800 − 10080

= 405720.

ii. all vowels together ?

In the word 'MAHARASHTRA' the number of letters is n = 11 of which A repeats 4 times, i.e., p = 4, H repeats twice i.e., q = 2, R repeats twice, i.e., r = 2 and rest are distinct.

∴ the number of different arrangements with the letters of the word MAHARASHTRA is

$\frac{n!}{p! q! r!}$

= $\frac{11!}{4! 2! 2!}$

= $\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4!}{4! \times 2 \times 1 \times 2 \times 1}$

= 11 × 10 × 9 × 2 × 7 × 6 × 5

= 415800

Vowels are A, A, A, A always together.

The number of arrangements of 4 vowels = $\frac{4!}{4!}$

= 1 ...(∵ A repeats 4 times.)

Considering 4 vowels as one unit (object), we have altogether 7 + 1 = 8 letters, i.e., n = 8 of which H repeats twice, i.e., p = 2 and R repeats twice, i.e., q = 2.

∴ number of possible arrangements of the letters of the word MAHARASHTRA in which all the vowels are together.

= $\frac{8!}{2! 2!} \times 1$

= $\frac{8!}{2! 2!}$

= $\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1}$

= 10080

Q.7 How many different words are formed if the letter R is used thrice and letters S and T are used twice each?

When ‘R’ is taken thrice, ‘S’ is taken twice and ‘T’ is taken twice,

∴ Total number of letters available = 7, of which ‘S’ and ‘T’ repeat 2 times each, ‘R’ repeats 3 times.

∴ Required number of arrangements = $\frac{7!}{2! 2! 3!}$

= $\frac{7 \times 6 \times 5 \times 4 \times 3!}{2 \times 1 \times 2 \times 1 \times 3!}$

= 7 × 6 × 5

= 210

∴ 210 different words can be formed when the letter R is used thrice and letters S and T are used twice each.

Q.8 Find the number of arrangements of letters in the word MUMBAI so that the letter B is always next to A.

In the word MUMBAI the number of letters is n = 6 of which M repeats twice, i.e., p = 2.

If B is always next to A, i.e., AB, then it forms one unit and remaining 4 letters. Therefore total number of letters n = 5 and p = 2.

∴ number of different ways of arrangements of letters in which B is always next to A

= $\frac{n!}{p!}$

= $\frac{5!}{2!}$

= $\frac{120}{2}$

= 60.

Q.9 Find the number of arrangements of letters in the word CONSTITUTION that begin and end with N.

There are 12 letters in the word CONSTITUTION, in which ‘O’, ‘N’, ‘I’ repeat two times each, ‘T’ repeats 3 times.

When the arrangement starts and ends with ‘N’, other 10 letters can be arranged between two N, in which ‘O’ and ‘I’ repeat twice each and ‘T’ repeats 3 times.

∴ Total number of arrangements with the letter N at the beginning and at the end = $\frac{10!}{2! 2! 3!}$

Q.10 Find the number of different ways of arranging letters in the word ARRANGE. How many of these arrngements do not have the two R's and two A's together?

In the word ARRANGE the number of letters is n = 7 of which A repeats twice, i.e., p = 2, R repeats twice, i.e., q = 2 and the rest are distinct.

∴ the number of ways in which the letters of the word 'ARRANGE' are arranged

= $\frac{n!}{p! q!}$

= $\frac{7!}{2! 2!}$

= $\frac{5040}{4}$

= 1260

Neither two R's nor two A's are together:

Let two R's and two A's occur together. Considering two R's as one unit and two A's as another unit we have 3 + 2 = 5 letters.

∴ number of arrangements of letters in which two R's and two A's are together = $\frac{5!}{2! 2!}$

= $\frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1}$

= 30

∴ number of arrangements in which neither two R's nor two A's are together

= 1260 – 30

= 1230

Q.11 How many distinct 5 digit numbers can be formed using the digits 3, 2, 3, 2, 4, 5.

5 digit numbers are to be formed from 2, 3, 2, 3, 4, 5.

Case I: Numbers formed from 2, 2, 3, 4, 5 OR 2, 3, 3, 4, 5

Number of such numbers = $\frac{5!}{2!} \times 2$

= 5!

= 120

Case II: Numbers are formed from 2, 2, 3, 3 and any one of 4 or 5

Number of such numbers = $\frac{5!}{2! 2!} \times 2$

= 60

Required number = 120 + 60

= 180

∴ 180 distinct 5 digit numbers can be formed using the digit 3, 2, 3, 2, 4, 5.

Q.12 Find the number of distinct numbers formed using the digits 3, 4, 5, 6, 7, 8, 9, so that odd positions are occupied by odd digits.

Digits are 3, 4, 5, 6, 7, 8, 9

Odd places are 1^st, 3^rd, 5^th and 7^th and odd digits are 3, 5, 7, 9. Even places are 2^nd, 4^th and 6^th and even digits are 2, 4, 6.

The four odd digits occupy 4 odd places in ⁴P₄ ways and three even digits can occupy the remaining 3 even places in ³P₃ ways.

∴ the total number of distinct numbers that can be formed

= ⁴P₄ × ³P₃ = 4!3!

= 4 × 3 × 2 × 1 × 3 × 2 × 1

= 144.

Q.13 How many different 6-digit numbers can be formed using digits in the number 659942? How many of them are divisible by 4?

A 6-digit number is to be formed using digits of 659942, in which 9 repeats twice.

∴ Total number of arrangements

= $\frac{6!}{2!}$

= $\frac{6 \times 5 \times 4 \times 3 \times 2!}{2!}$

= 360

∴ 360 different 6-digit numbers can be formed.

For a number to be divisible by 4, the last two digits should be divisible by 4 i.e. 24, 52, 56, 64, 92, or 96.

Case I: When the last two digits are 24, 52, 56 or 64.

As the digit 9 repeats twice in the remaining four numbers, the number of arrangements

= $\frac{4!}{2!}$

= 12

∴ 6-digit numbers that are divisible by 4 so formed are 12 + 12 + 12 + 12 = 48.

Case II: When the last two digits are 92 or 96.

As each of the remaining four numbers is distinct, the number of arrangements = 4! = 24

∴ 6-digit numbers that are divisible by 4 so formed are 24 + 24 = 48.

∴ Total number of arrangements from both these cases is 48 + 48 = 96.

Thus, 96 6-digit numbers can be formed that are divisible by 4.

Q.14 Find the numbers of distinct words formed from letters in the word INDIAN. How many of them have the two N's together?

In the word 'INDIAN', the number of letters is n = 6 of which I repeats twice, i.e., p = 2, N repeats twice, i.e., q = 2, and the rest are distinct.

∴ the number of different words formed with letters of the word INDIAN

= $\frac{n!}{p! q!}$

= $\frac{6!}{2! 2!}$

= $\frac{6 \times 5 \times 4 \times 3 \times 2!}{2 \times 1 \times 2!}$

= 180

Two N's are together:

Two N's form 1 unit and with the remaining 4 letters we have 5 letters in which I repeat twice.

∴ the number of different words formed in which two N's are together

= $\frac{5!}{2!}$

= $\frac{5 \times 4 \times 3 \times 2!}{2!}$

= 60

Q.15 Find the number of different ways of arranging letters in the word PLATOON if :

i. the two O's are never together.

When the two O’s are never together

Let us arrange the other 5 letters first, which can be done in 5! = 120 ways.

The letters P, L, A, T, N create 6 gaps, in which O’s are arranged.

Two O’s can take their places in ⁶P₂ ways.

But ‘O’ repeats 2 times.

∴ Two O’s can be arranged in $\frac{^{6} P_{2}}{2!}$

= $\frac{\frac{6!}{(6 - 2)!}}{2!}$

= $\frac{6 \times 5 \times 4!}{4! \times 2 \times 1}$

= 3 × 5

= 15 ways

∴ Total number of arrangements if the two O’s are never together = 120 × 15 = 1800

ii. consonants and vowels occupy alternate positions.

In the word 'PLATOON', the number of letters is n = 7 of which 'O' repeats twice, i.e., p = 2

∴ the total number of words formed by using the letters of the word 'PLATOON'

= $\frac{n!}{p!}$

= $\frac{7!}{2!}$

= $\frac{7 \times 6 \times 5 \times 4 \times 3 \times 2!}{2!}$

= 2520

Consonants and Vowels occupy alternate positions:

There are 4 consonants P, L, T, N, and three vowels A, O, O.

The possible arrangement in which consonants and vowels take alternate places is CVCVCVC.

Three vowels can be arranged at three places in $\frac{3!}{2!}$ ways (∵ O repeats twice) and four consonants can be arranged at 4 places in 4! ways.

∴ the number of such arrangements

= $\frac{3!}{2!} \times 4!$

= $\frac{3 \times 2!}{2!} \times 4 \times 3 \times 2 \times 1$

= 72

Exercise 3.5

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9 Q.10

Q.1 In how many different ways can 8 friends sit around a table ?

We know that ‘n’ persons can sit around a table in (n – 1)! ways

∴ 8 friends can sit around a table in 7! ways

= 7 × 6 × 5 × 4 × 3 × 2 × 1

= 5040 ways.

∴ 8 friends can sit around a table in 5040 ways.

Q.2 A party has 20 participants. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host ?

Here, n = Total number of participants = 20 + 1 host = 21

∴ the number of ways in which these 21 persons can be seated at a circular table = (n – 1)!

= (21 – 1)!

= 20!

Taking 2 specified persons and host as 1 unit, there are 18 + 1 = 19 persons.

Now 19 persons can be arranged in (19 – 1)! = 18! ways.

The host always occupies the centre position and two specified persons be seated on either side of the host in 2! ways.

Hence, the total number of circular arrangements in which two specified persons be seated on either side of the host = 18! × 2! = 2(18!).

Q.3 Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangements where two specified delegates are :

i. always together :

Delegates of 24 countries are to be participate in a round table discussion such that two specified delegates are always together.

Let us consider these 2 delegates as one unit. They can be arranged among themselves in 2! ways.

Also, these two delegates are to be seated with 22 other delegates (i.e. total 23) which can be done in (23 – 1)! = 22! ways.

∴ Total number of arrangement possible if two specified delegates are always together = 22! × 2!

ii. never together :

Here, n = No. of delegates = 24

∴ 24 delegates can be seated at the round table in (n – 1)! ways

= (24 – 1)!

= 23! ways

Two particular delegates are never together :

The number of circular arrangements of delegates in which two particular delegates are never together

= $[\begin{matrix} Total number of \\ circular arrangements \\ of 24 delegates \end{matrix}] - [\begin{matrix} Total number of circular \\ arrangements which two particular \\ delegates are always together \end{matrix}]$

= 23! – (22! × 2!)

= 23 × 22! – 22! × 2

= 22!(23 – 2)

= 21 × 22!.

Q.4 Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.

There are 15 people to sit around a table.

∴ They can be arranged in (15 – 1)! = 14! ways.

But, they should not have the same neighbour in any two arrangements.

Around table, arrangements (i.e. clockwise and anticlock wise) coincide.

diagram

∴ No. of arrangements possible for not to have same neighbours = $\frac{14!}{2}$

Q.5 A committee of 10 members sits around a table. Find the number of arrangements that have the President and the Vice-president together.

Here, n = No. of committee members = 10

Consider 'President' and 'Vice-President' as one unit.

So there are 1 + 8 = 9 members to be arranged around a table.

Such arrangements are (9 – 1)! = 8! and corresponding to each of these 8! arrangements, the President and the Vice-President can interchange their places in 2! ways.

∴ the total number of circular arrangements of 10 committee members in which President and Vice-President sit together

= 8! × 2!

= 2(8!)

Q.6 Five men, two women and a child sit around a table. Find the number of arrangements where the child is seated :

i. between the two women :

5 men, 2 women and a child sit around a table.

When child is seated between two women.

5 men, 2 women and a child are to be seated around a round table such that the child is seated between two women.

∴ the two women can be seated on either side of the child in 2! ways.

Let us consider these 3 (two women and a child) as one unit

Also, these 3 are to seated with 5 men

(i.e. total 6 unit) which can be done in (6 – 1)! = 5! ways.

∴ Total number of arrangements if child is seated between two women

= 5! × 2!

= 120 × 2

= 240

ii. between two men :

Here, 5 men + 2 women + 1 child = 8 people.

Child is seated between two men:

Two men can be selected from the five men (M₁, M₂, M₃, M₄, M₅) in 10 ways as follows:

(M₁M₂, M₁M₃, M₁M₄, M₁M₅, M₂M₃, M₂M₄, M₂M₅, M₃M₄, M₃M₅, M₄M₅)

Consider 2 men and a child as one group. These two men can be arranged so that the child is in between the men, in ²P₂ = 2! ways.

Now the group of 2 men and a child, the remaining 3 men and 2 women, i.e., altogether 6 persons can be arranged around the table in (6 – 1)! = 5! ways.

∴ the number of ways of arranging eight people such that the child is seated between two men

= 10 × 2! × 5!

= 10 × 2 × 1 × 5 × 4 × 3 × 2 × 1

= 2400

Q.7 Eight men and six women sit around a table. How many of sitting arrangements will have no two women together ?

8 men can be seated around a table in (8 – 1)! = 7! ways.

There are 8 gaps created by 8 men’s seats.

∴ Women can be seated in 8 gaps in ⁸P₆ ways

∴ Total number of arrangements so that no two women are together = 7! × ⁸P₆

Q.8 Find the number of seating arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.

We can choose 2 women from 3 women in 3 ways. (W₁W₂, W₁W₃, W₂W₃).

After choosing 2 women, consider them as 1 group.

Also, we have remaining 1 woman and 3 men.

Thus, we have 1 + 1 + 3 = 5 persons to be seated around the table.

These 5 persons can be seated around the table in (5 – 1) = 4! ways and corresponding to each of these 4! arrangements, the 2 women can interchange their seats in 2! ways.

∴ the number of seating arrangements for 3 men and 3 women around a table so that exactly 2 women are together

= 3 × 4! × 2!

= 3 × 4 × 3 × 2 × 1 × 2 × 1

= 144.

Q.9 Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order.

Ten things can be arranged in a circular order of which 4 are alike in $\frac{9!}{4!}$ ways 4 are alike.

∴ Total number of ways arrangement can be done

= $\frac{9!}{4!}$

Q.10 Fifteen persons sit around a table. Find the number of arrangement that have two specified persons not sitting side by side.

Here, n = 15

15 persons are arranged around the table in (15 – 1)! = 14! ways.

Let two particular persons sit together.

∴ the number of ways in which 15 persons are arranged around the table such that two particular persons sit together is = 13! × 2!

Hence, the number of ways in which 15 persons are arranged around the table such that two particular persons are not to be side by side

= 14! – 13! × 2!

= 14 × 13! – 13! × 2

= 13!(14 – 2)

= 12 × 13!

Exercise 3.6

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9 Q.10 Q.11 Q.12 Q.13 Q.14 Q.15 Q.16 Q.17 Q.18 Q.19 Q.20 Q.21 Q.22 Q.23 Q.24 Q.25 Q.26

Q.1 Find the value of :

i. ¹⁵C₄ :

¹⁵C₄ = $\frac{15!}{4! (15 - 4)!}$

= $\frac{15!}{4! 11!}$

= $\frac{15 \times 14 \times 13 \times 12 \times 11!}{4 \times 3 \times 2 \times 1 \times 11!}$

= $\frac{15 \times 14 \times 13 \times 12}{4 \times 3 \times 2 \times 1}$

= 1365

ii. ⁸⁰C₂ :

⁸⁰C₂ = $\frac{80!}{2! (80 - 2)!}$

= $\frac{80!}{2! 78!}$

= $\frac{80 \times 79 \times 78!}{2 \times 78!}$

= 40 × 79

= 3160

iii. ¹⁵C₄ + ¹⁵C_{5 :}

¹⁵C₄ + ¹⁵C₅

= ¹⁵C₅ +¹⁵C₄

= ¹⁵C₅ + ¹⁵C_5–1

= ¹⁶C₅ ...[∵ ⁿC_r + ⁿC_r–1 = ⁿ⁺¹C_r]

iv. ²⁰C₁₆ – ¹⁹C₁₆ :

²⁰C₁₆ – ¹⁹C₁₆

= ¹⁹C₁₆ + ¹⁹C₁₅ – ¹⁹C₁₆ ...[∵ ⁿC_r + ⁿC_r–1 = ⁿ⁺¹C_r]

= $\frac{19!}{15! (19 - 15)!}$

= $\frac{19!}{15! 4!}$

= $\frac{19 \times 18 \times 17 \times 16 \times 15!}{15! \times 4 \times 3 \times 2 \times 1}$

= 19 × 6 × 17 × 2

= 3876

∴ ²⁰C₁₆ – ¹⁹C₁₆ = ¹⁹C₁₅ = 3876

Q.2 Find n if :

i. ⁶P₂ = n ⁶C₂

⁶P₂ = n ⁶C₂

∴ $\frac{6!}{(6 - 2)!} = n \frac{6!}{2! (6 - 2)!}$

∴ $\frac{6!}{4!} = n \frac{6!}{2! 4!}$

∴ n = 2!

= 2 × 1

= 2

ii. ²ⁿC₃ : ⁿC₂ = 52 : 3

²ⁿC₃ : ⁿC₂ = 52 : 3

= ⁵P₅

∴ $\frac{^{2 n} C_{3}}{^{n} C_{2}} = \frac{52}{3}$

∴ $\frac{2 n!}{3! (2 n - 3)!} \times \frac{2! (n - 2)!}{n!} = \frac{52}{3}$

∴ $\frac{2 n (2 n - 1) (2 n - 2) (2 n - 3)!}{3 \times 2 \times 1 \times (2 n - 3)!} \times \frac{2 \times 1 \times (n - 2)!}{n (n - 1) (n - 2)!} = \frac{52}{3}$

∴ $\frac{2 \times n \times (2 n - 1) 2 (n - 1)}{3 \times 2 \times 1} \times \frac{2 \times 1}{n (n - 1)} = \frac{52}{3}$

∴ $\frac{52}{4}$

∴ 2n – 1 = 13

∴ 2n = 14

∴ n = 7.

iii. ⁿC_n–3 = 84

ⁿC_n–3 = 84

∴ $\frac{n!}{(n - 3)! [n - (n - 3)]!}$ = 84

∴ $\frac{n (n - 1) (n - 2) (n - 3)!}{(n - 3)! \times 3!}$ = 84

∴ n(n – 1)(n – 2) = 84 × 6

∴ n(n – 1)(n – 2) = 9 × 8 × 7

Comparing on both sides, we get n = 9

Q.3 Find r if ¹⁴C_2r : ¹⁰C_2r–4 = 143 : 10.

¹⁴C_2r : ¹⁰C_2r–4 = 143 : 10

∴ $\frac{14!}{2 r! (14 - 2 r)!} \times \frac{(2 r - 4)! (10 - 2 r + 4)!}{10!} = \frac{143}{10}$

∴ $\frac{14 \times 13 \times 12 \times 11 \times 10!}{2 r (2 r - 1) (2 r - 2) (2 r - 3) (2 r - 4)! \times (14 - 2 r)!} \times \frac{(2 r - 4)! \times (14 - 2 r)!}{10!} = \frac{143}{10}$

∴ $\frac{14 \times 13 \times 12 \times 11}{2 r (2 r - 1) (2 r - 2) (2 r - 3)} = \frac{143}{10}$

∴ $\frac{14 \times 12 \times 143}{2 r (2 r - 1) (2 r - 2) (2 r - 3)} = \frac{143}{10}$

∴ 14 × 12 × 10 = 2r(2r – 1)(2r – 2)(2r – 3)

∴ 2r(2r – 1)(2r – 2)(2r – 3) = 1680

∴ 2r(2r – 1)(2r – 2)(2r – 3) = 8 × 7 × 6 × 5

∴ 2r(2r – 1)(2r – 2)(2r – 3) = 8(8 – 1)(8 – 2)(8 – 3)

∴ 2r = 8 .........(by observation)

∴ r = 4.

Q.4 Find n and r if :

i. ⁿP_r = 720 and ⁿC_n–r = 120

ⁿP_r = 720

∴ $\frac{n!}{(n - r)!}$ = 720 ...(i)

Also, ⁿC_n–r = 120

∴ $\frac{n!}{(n - r)! (n - n + r)!}$ = 120

∴ $\frac{n!}{r! (n - r)!}$ = 120 ...(ii)

Dividing (i) by (ii), we get

$\frac{\frac{n!}{(n - r)!}}{\frac{n!}{r! (n - r)!}} = \frac{720}{120}$

∴ r! = 6

∴ r = 3

Substituting r = 3 in (i), we get

$\frac{n!}{(n - 3)!}$

∴ $\frac{n (n - 1) (n - 2) (n - 3)!}{(n - 3)!}$ = 720

∴ n(n – 1) (n – 2) = 10 × 9 × 8

∴ n = 10

ii. Find n and r if ⁿC_r–1 : ⁿC_r : ⁿC_r+1 = 20 : 35 : 42

ⁿC_r–1 : ⁿC_r : ⁿC_r+1 = 20 : 35 : 42

∴ ⁿC_r–1 : ⁿC_r = 20 : 35 and

ⁿC_r : ⁿC_r+1 = 35 : 42

Take, ⁿC_r–1 : ⁿC_r = 20 : 35

∴ $\frac{n!}{(r - 1)! (n - r + 1)!} \times \frac{r! (n - r)!}{n!} = \frac{20}{35}$

∴ $\frac{1}{(r - 1)! (n - r + 1) (n - r)!} \times r (r - 1)! (n - r)! = \frac{20}{35}$

∴ $\frac{r}{n - r + 1} = \frac{20}{35}$

∴ 35r = 20n – 20r + 20

∴ 55r – 20n = 20

∴ 11r – 4n = 4 ...(1)

Take ⁿC_r : ⁿC_r+1 = 35 : 42

∴ $\frac{n!}{r! (n - r)!} \times \frac{(r + 1)! (n - r - 1)!}{n!} = \frac{35}{42}$

∴ $\frac{(r + 1) \times r! \times (n - r - 1)!}{r! (n - r) (n - r - 1)!} = \frac{35}{42}$

∴ $\frac{r + 1}{n - r} = \frac{5}{6}$

∴ 6r + 6 = 5n – 5r

∴ 11r – 5n = – 6 ...(2)

Subtracting equation (2) from equation (1), we get,

11r – 4n = 4
11r – 5n = – 6
– + +
∴ n = 10

Putting n = 10 in the equation (1), we get,

11r – 4(10) = 4

∴ 11r – 40 = 4

∴ 11r = 44

∴ r = 4

Hence, n = 10 and r = 4.

Q.5 If ⁿP_r = 1814400 and ⁿC_r = 45, find ⁿ⁺⁴C_r+3

ⁿP_r = 1814400, ⁿC_r = 45

∴ $\frac{^{n} P_{r}}{^{n} C_{r}} = \frac{1814400}{45}$

∴ $\frac{n!}{(n - r)!} \times \frac{r! (n - r)!}{n!} = \frac{1814400}{45}$

∴ r! = 40320

∴ r! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

∴ r! = 8!

∴ r = 8

Also, ⁿC_r = 45

∴ ⁿC₈ = 45

∴ $\frac{n!}{8! (n - 8)!}$ = 45

∴ n(n – 1)(n – 2)(n – 3)(n – 4)(n – 5)(n – 6) (n – 7) = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3

Comparing on both sides, we get

n = 10

∴ ⁿ⁺⁴C_r+3 = ¹⁴C₁₁

= $\frac{14!}{11! (14 - 11)!}$

= $\frac{14!}{11! 3!}$

= $\frac{14 \times 13 \times 12 \times 11!}{11! \times 3 \times 2 \times 1}$

= 364

Q.6 If ⁿC_r–1 = 6435, ⁿC_r = 5005, ⁿC_r+1 = 3003, find ^rC₅.

ⁿC_r–1 = 6435, ⁿC_r = 5005, ⁿC_r+1 = 3003

∴ $\frac{^{n} C_{r - 1}}{^{n} C_{r}} = \frac{6435}{5005} = \frac{9}{7}$

∴ $\frac{n!}{(r - 1)! (n - r + 1)!} \times \frac{r! (n - r)!}{n!} = \frac{9}{7}$

∴ $\frac{r (r - 1)! (n - r)!}{(r - 1)! (n - r + 1) (n - r)!} = \frac{9}{7}$

∴ $\frac{r}{n - r + 1} = \frac{9}{7}$

∴ 7r = 9n – 9r + 9

∴ 16r – 9n = 9 ...(1)

Also, $\frac{^{n} C_{r}}{^{n} C_{r + 1}} = \frac{5005}{3003} = \frac{5}{3}$

∴ $\frac{n!}{r! (n - r)!} \times \frac{(r + 1)! (n - r - 1)!}{n!} = \frac{5}{3}$

∴ $\frac{(r + 1) r! (n - r - 1)!}{r! (n - r) (n - r - 1)!} = \frac{5}{3}$

∴ $\frac{r + 1}{n - r} = \frac{5}{3}$

∴ 3r + 3 = 5n − 5r

∴ 8r – 5n = – 3 ...(2)

Multiplying equation (1) by 5 and equation (2) by 9, we get,

80r – 45n = 45

72r – 45n = – 27

On subtracting, we get,

8r = 72

∴ r = 9

∴ ^rC₅ = ⁹C₅ = $\frac{9!}{5! 4!}$

= $\frac{9 \times 8 \times 7 \times 6 \times 5!}{5! \times 4 \times 3 \times 2 \times 1}$

= 126

Q.7 Find the number of ways of drawing 9 balls from a bag that has 6 red balls, 8 green balls and 7 blue balls so that 3 balls of every colour are drawn.

9 balls are to be selected from 6 red, 8 green, 7 blue balls such that the selection consists of 3 balls of each colour.

∴ 3 red balls can be selected from 6 red balls in ⁶C₃ ways.

3 green balls can be selected from 8 green balls in ⁸C₃ ways.

3 blue balls can be selected from 7 blue balls in ⁷C₃ ways.

∴ Number of ways selection can be done if the selection consists of 3 balls of each colour

= ⁶C₃. ⁸C₃. ⁷C₃

= $\frac{6!}{3! 3!} \times \frac{8!}{3! 5!} \times \frac{7!}{3! 4!}$

= $\frac{6 \times 5 \times 4 \times 3!}{3 \times 2 \times 1 \times 3!} \times \frac{8 \times 7 \times 6 \times 5!}{3 \times 2 \times 1 \times 5!} \times \frac{7 \times 6 \times 5 \times 4!}{3 \times 2 \times 1 \times 4!}$

= 20 × 56 × 35

= 39200

Q.8 Find the number of ways of selecting a team of 3 boys and 2 girls from 6 boys and 4 girls.

There are 6 boys and 4 girls.

∴ the number of ways in which 3 boys and 2 girls can be selected

= ⁶C₃ × ⁴C₂

= $\frac{6!}{3! 3!} \times \frac{4!}{2! 2!}$

= $\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times \frac{4 \times 3}{2 \times 1}$

= 20 × 6

= 120.

Q.9 After a meeting, every participant shakes hands with every other participants. If the number of handshakes is 66, find the number of participants in the meeting.

Let there be n participants present in the meeting.

A handshake occurs between 2 persons.

∴ Number of handshakes = ⁿC₂

Given 66 handshakes were exchanged.

∴ 66 = ⁿC₂

∴ 66 = $\frac{n!}{2! (n - 2)!}$

∴ 66 × 2 = $\frac{n (n - 1) (n - 2)!}{(n - 2)!}$

∴ 132 = n(n – 1)

∴ n(n – 1) = 12 × 11

Comparing on both sides, we get

n = 12

∴ 12 participants were present at the meeting.

Q.10 If 20 points are marked on a circle, how many chords can be drawn ?

There are 20 points on a circle.

To draw a chord, 2 points are required.

∴ the number of chords that can be drawn through 20 points on the circle

= ²⁰C₂

= $\frac{20!}{2! 18!}$

= $\frac{20 \times 19 \times 18!}{2 \times 1 \times 18!}$

= 190.

Q.11 Find the number of diagonals of an n-sided polygon. In particular, find the number of diagonals when :

i. n = 10

In an n-sided polygon, there are ‘n’ points and ‘n’ sides.

∴ Through ‘n’ points we can draw ⁿC₂ lines including sides.

∴ Number of diagonals in n sided polygon

= ⁿC₂ – n .........(n = number of sides)

n = 10

ⁿC₂ – n = ¹⁰C₂ – 10

= $\frac{10 \times 9}{1 \times 2} - 10$

= 45 – 10

= 35

ii. n = 15

There are n vertices in the polygon of n-sides.

If we join any two vertices, we get either side or the diagonal of the polygon.

Two vertices can be joined in ⁿC₂ ways.

∴ total number of sides and diagonals = ⁿC₂

But there are n sides in the polygon.

∴ total number of the diagonals = ⁿC₂ – n

n = 15 sides

∴ the number of diagonal that can be drawn

= ¹⁵C₂ – 15

= $\frac{15!}{2! 13!} - 15$

= $\frac{15 \times 14 \times 13!}{2 \times 13!} - 15$

= $\frac{15 \times 14}{2} - 15$

= 105 – 15

= 90

iii. n = 12

In an n-sided polygon, there are ‘n’ points and ‘n’ sides.

∴ Through ‘n’ points we can draw ⁿC₂ lines including sides.

∴ Number of diagonals in n sided polygon

= ⁿC₂ – n ...(n = number of sides)

n = 12, ⁿC₂ – n = ¹²C₂ – 12

= $\frac{12 \times 11}{1 \times 2} - 12$

= 66 – 12

= 54

iv. n = 8

There are n vertices in the polygon of n-sides.

If we join any two vertices, we get either side or the diagonal of the polygon.

Two vertices can be joined in ⁿC₂ ways.

∴ total number of sides and diagonals = ⁿC₂

But there are n sides in the polygon.

∴ total number of the diagonals = ⁿC₂ – n

n = 8 sides

∴ the number of diagonals that can be drawn

= ⁸C₂ – 8

= $\frac{8!}{2! 6!} - 8$

= $\frac{8 \times 7 \times 6!}{2 \times 6!} - 8$

= 28 – 8

= 20

Q.12 There are 20 straight lines in a plane so that no two lines are parallel and no three lines are concurrent. Determine the number of points of intersection.

There are 20 lines such that no two of them are parallel and no three of them are concurrent.

Since no two lines are parallel

∴ they intersect at a point

∴ Number of points of intersection if no two lines are parallel and no three lines are concurrent

= ²⁰C₂

= $\frac{20!}{2! 18!}$

= $\frac{20 \times 19 \times 18!}{2 \times 1 \times 18!}$

= 190

Q.13 Ten points are plotted on a plane. Find the number of straight lines obtained by joining these point if :

i. no three points are collinear :

A line is drawn by joining 2 points from the given 10 points.

∴ number of straight lines

= ¹⁰C₂

= $\frac{10!}{2! 8!}$

= $\frac{10 \times 9 \times 8!}{2 \times 8!}$

= 45, if no three points are collinear.

ii. four points are collinear :

There are 10 points on a plane.

When 4 of them are collinear

∴ Number of lines passing through these points if 4 points are collinear

= ¹⁰C₂ – ⁴C₂ + 1

= $45 - \frac{4!}{2! 2!} + 1$

= $45 - \frac{4 \times 3 \times 2!}{2 \times 2!} + 1$

= 45 – 6 + 1

= 40

Q.14 Find the number of triangles formed by joining 12 points if :

i. no three points are collinear :

A triangle can be formed by selecting 3 non-collinear points.

We can choose 3 points from 12 points in

¹²C₃ = $\frac{12!}{3! 9!}$

= $\frac{12 \times 11 \times 10 \times 9!}{3 \times 2 \times 1 \times 9!}$

= 220 ways

∴ number of triangles = 220.

ii. four points are collinear :

There are 12 points on the plane

When 4 of these points are collinear

∴ Number of triangles that can be obtained from these points = ¹²C₃ – ⁴C₃

= $220 - \frac{4!}{3! \times 1!}$

= $220 - \frac{4 \times 3!}{3!}$

= 220 – 4

= 216

Q.15 A word has 8 consonants and 3 vowels. How many distinct words can be formed if 4 consonants and 2 vowels are chosen ?

4 consonants can be selected from 8 consonants in ⁸C₄ ways and 2 vowels can be selected from 3 vowels in ³C₂ ways.

∴ the number of words with 4 consonants and 2 vowels = ⁸C₄ × ³C₂

= $\frac{8!}{4! 4!} \times \frac{3!}{2! 1!}$

= $\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} \times \frac{3 \times 2!}{2!}$

= 70 × 3

= 210

Now each of these words contains 6 letters which can be arranged in ⁶P₆ = 6! ways.

∴ the total number of words that can be formed with 4 consonants and 2 vowels

= 210 × 6!

= 210 × 6 × 5 × 4 × 3 × 2 × 1

= 151200.

Q.16 Find n if :

i. ⁿC₈ = ⁿC₁₂

ⁿC₈ = ⁿC₁₂

If ⁿC_x = ⁿC_y, then either x = y or x = n – y

∴ 8 = 12 or 8 = n – 12

But 8 = 12 is not possible

∴ 8 = n – 12

∴ n = 20

ii. ²³C_3n = ²³C_2n+3

²³C_3n = ²³C_2n+3

We know that if ⁿC_x = ⁿC_y, then x = y or x + y = n

∴ 3n = 2n + 3 or 3n + 2n + 3 = 23

∴ n = 3 or 5n = 20

∴ n = 3 or n = 4.

iii. ²¹C_6n = $^{21} C_{(n^{2} + 5)}$

²¹C_6n = $^{21} C_{(n^{2} + 5)}$

If ⁿC_x = ⁿC_y, then either x = y or x = n – y

∴ 6n = n² + 5 or 6n = 21 – (n² + 5)

∴ n² – 6n + 5 = 0 or 6n = 21 – n² – 5

∴ n² – 6n + 5 = 0 or n² + 6n – 16 = 0

If n² – 6n + 5 = 0 then (n – 1)(n – 5) = 0

∴ n = 1 or n = 5

If n = 5 then

n² + 5 = 30 > 21

∴ n ≠ 5

∴ n = 1

If n² + 6n – 16 = 0 then (n + 8)(n – 2) = 0

n = – 8 or n = 2

n ≠ – 8

∴ n = 2

iv. ²¹C_6n = $^{21} C_{(n^{2} + 5)}$

²¹C_6n = $^{21} C_{(n^{2} + 5)}$

If ⁿC_x = ⁿC_y, then either x = y or x = n – y

∴ 6n = n² + 5 or 6n = 21 – (n² + 5)

∴ n² – 6n + 5 = 0 or 6n = 21 – n² – 5

∴ n² – 6n + 5 = 0 or n² + 6n – 16 = 0

If n² – 6n + 5 = 0 then (n – 1)(n – 5) = 0

∴ n = 1 or n = 5

If n = 5 then

n² + 5 = 30 > 21

∴ n ≠ 5

∴ n = 1

If n² + 6n – 16 = 0 then (n + 8)(n – 2) = 0

n = – 8 or n = 2

n ≠ – 8

∴ n = 2

v. ²ⁿC_r–1 = ²ⁿC_r+1

ⁿC_n–2 = 15

∴ ⁿC₂ = 15 ...[∵ ⁿC_r = ⁿC_n–r]

∴ $\frac{n!}{(n - 2)! 2!}$ = 15

∴ $\frac{n (n - 1) (n - 2)!}{(n - 2)! 2 \times 1}$ = 15

∴ n(n – 1) = 30

∴ n(n – 1) = 6 × 5

Equating both sides, we get

∴ n = 6

Q.17 Find x if ⁿP_r = x ⁿC_r

ⁿP_r = x ⁿC_r

We know that ⁿC_r = $\frac{^{n} P_{r}}{r!}$

∴ ⁿP_r = $x \times \frac{^{n} P_{r}}{r!}$

∴ 1 = $\frac{x}{r!}$

∴ x = r!

Q.18 Find r if ¹¹C₄ + ¹¹C₅ + ¹²C₆ + ¹³C₇ = ¹⁴C_r

¹¹C₄ + ¹¹C₅ + ¹²C₆ + ¹³C₇ = ¹⁴C_r

∴ (¹¹C₄ + ¹¹C₅) + ¹²C₆ + ¹³C₇ = ¹⁴C_r ...[ⁿC_r + ⁿC_r–1 = ⁿ⁺¹C_r]

∴ (¹²C₅ + ¹²C₆) + ¹³C₇ = ¹⁴C_r

∴ (¹³C₆ + ¹³C₇) = ¹⁴C_r

∴ ¹⁴C₇ = ¹⁴C_r

If ⁿC_x = ⁿC_y, then either x = y or x = n – y

∴ r = 7 or r = 14 – 7 = 7

Q.19 Find the value of $\sum_{r = 1}^{4}^{(21 - r)} C_{4}$

$\sum_{r = 1}^{4}^{(21 - r)} C_{4} =^{(21 - 1)} C_{4} +^{(21 - 2)} C_{4} +^{(21 - 3)} C_{4} +^{(21 - 4)} C_{4}$

= ²⁰C₄ + ¹⁹C₄ + ¹⁸C₄ + ¹⁷C₄

= ²⁰C₄ + ¹⁹C₄ + ¹⁸C₄ + ¹⁸C₅ – ¹⁷C₅ ...[∵ ⁿC_r + ⁿC_r–1 = ⁿ⁺¹C_r ∴ ⁿC_r–1 = ⁿ⁺¹C_r – ⁿC_r]

= ²⁰C₄ + ¹⁹C₄ + ¹⁹C₅ – ¹⁷C₅ ...[∵ ⁿC_r + ⁿC_r–1 = ⁿ⁺¹C_r]

= ²⁰C₄ + ²⁰C₅ – ¹⁷C₅

= ²¹C₅ – ¹⁷C₅

= $\frac{2!}{5! 16!} - \frac{17!}{5! 12!}$

= $\frac{21 \times 20 \times 19 \times 18 \times 17 \times 16!}{5 \times 4 \times 3 \times 2 \times 1 \times 16!} - \frac{17 \times 16 \times 15 \times 14 \times 13 \times 12!}{5 \times 4 \times 3 \times 2 \times 1 \times 12!}$

= 21 × 19 × 3 × 17 – 17 × 2 × 14 × 13

= 20349 – 6188

= 14161

Q.20 Find the differences between the greatest values in the following :

i. ¹⁴C_r and ¹²C_r

Greatest value of ¹⁴C_r

Here n = 14, which is even

Greatest value of ⁿC_r occurs at r = $\frac{n}{2}$ if n is even

∴ r = $\frac{n}{2}$

∴ r = $\frac{14}{2}$ = 7

∴ Greatest value of ¹⁴C_r = ¹⁴C₇ = $\frac{14!}{7! 7!}$

= $\frac{14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7!}{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \times 7!}$

= 3432

Also, for greatest value of ¹²C_r

n = 12, which is even

∴ r = $\frac{12}{2}$ = 6

∴ ¹²C₆ = $\frac{12!}{6! 6!}$

= $\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6!}{6 \times 5 \times 4 \times 3 \times 2 \times 1 \times 6!}$

= 924

∴ Difference between the greatest values of ¹⁴C_r and ¹²C_r

= ¹⁴C_r and ¹²C_r

= 3432 – 924

= 2508

ii. ¹³C_r and ⁸C_r

The greatest value of ⁿC_r occurs at r = $\frac{n}{2}$ , if n is even and at r = $\frac{n - 1}{2}$ , if n is odd.

The greatest value of ¹³C_r occurs at

r = $\frac{13 - 1}{2}$ = 6 ...[∵ n = 13 is odd]

∴ the greatest value of ¹³C_r

= ¹³C₆

= $\frac{13!}{6! 7!}$

= $\frac{13 \times 12 \times 11 \times 10 \times 9 \times 8}{6 \times 5 \times 4 \times 3 \times 2 \times 1}$

= 13 × 11 × 2 × 3 × 2

= 1716

The greatest value of ⁸C_r occurs at

r = $\frac{8}{2}$ = 4 ...[∵ n = 8 is even]

∴ the greatest value of ⁸C_r

= ⁸C₄

= $\frac{8!}{4! 4!}$

= $\frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1}$

= 7 × 2 × 5

= 70

∴ the difference between the greatest values of ¹³C_r and ⁸C_r

= 1716 – 70

= 1646

iii. ¹⁵C_r and ¹¹C_r

Greatest value of ¹⁵C_r

Here n = 15, which is odd

Greatest value of ⁿC_r occurs at r = $\frac{n - 1}{2}$ if n is odd

∴ r = $\frac{15 - 1}{2}$ = 7

∴ Greatest value of ¹⁵C_r

= ¹⁵C₇

= $\frac{15!}{7! 8!}$

= $\frac{15 \times 14 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8!}{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \times 8!}$

= 6435

Also, for greatest value of ¹¹C_r

n = 11, which is odd

∴ r = $\frac{11 - 1}{2}$ = 5

∴ ¹¹C₅ = $\frac{11!}{5! 6!}$

= $\frac{11 \times 10 \times 9 \times 8 \times 7 \times 6!}{5 \times 4 \times 3 \times 2 \times 1 \times 6!}$

= 462

∴ Difference between the greatest values of ¹⁵C_r and ¹¹C_r

= ¹⁵C_r – ¹¹C_r

= 6435 – 462

= 5973

Q.21 In how many ways can a boy invite his 5 friends to a party so that at least three join the party ?

Number of friends n = 5.

At least three join the party

∴ r ≥ 3

∴ the number of ways in which a boy can invite 5 friends so that at least three join the party

= ⁵C₃ + ⁵C₄ + ⁵C₅

= $\frac{5!}{3! 2!} + \frac{5!}{4! 1!} + \frac{5!}{5! 0!}$

= $\frac{5 \times 4 \times 3!}{1 \times 2 \times 3!} + \frac{5 \times 4!}{4!} + 1$

= 10 + 5 + 1

= 16.

Q.22 A group consists of 9 men and 6 women. A team of 6 is to be selected. How many of possible selections will have at least 3 women ?

There are 9 men and 6 women.

A team of 6 persons is to be formed such that it consists of at least 3 women.

Consider the following table:

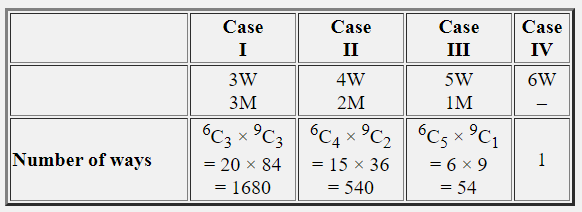
table

∴ No. of ways this can be done

= 1680 + 540 + 54 + 1

= 2275

∴ 2275 teams can be formed if the team consists of at least 3 women.

Q.23 A committee of 10 persons is to be formed from a group of 10 women and 8 men. How many possible committees will have at least 5 women? How many possible committees will have men in majority ?

There are 10 women and 8 men.

A committee of 10 persons is to be formed. If at least 5 women have been included in a committee, then the possible selection are :

5 women and 5 men, 6 women and 4 men,

7 women and 3 men, 8 women and 2 men,

9 women and 1 man and all the 10 women and no man.

∴ the number of ways of forming committees such that at least five women are included

= ¹⁰C₅ × ⁸C₅ + ¹⁰C₆ × ⁸C₄ + ¹⁰C₇ × ⁸C₃ + ¹⁰C₈ × ⁸C₂ + ¹⁰C₉ × ⁸C₁ + ¹⁰C₁₀ × ⁸C₀

= $\frac{10!}{5! 5!} \times \frac{8!}{5! 3!} + \frac{10!}{6! 4!} \times \frac{8!}{4! 4!} + \frac{10!}{7! 3!} \times \frac{8!}{3! 5!} + \frac{10!}{8! 2!} \times \frac{8!}{2! 6!} + \frac{10!}{9! 1!} \times \frac{8!}{1! 7!} + \frac{10!}{10! 0!} \times \frac{8!}{0! 8!}$

= $(\frac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2 \times 1} \times \frac{8 \times 7 \times 6}{1 \times 2 \times 3}) + (\frac{10 \times 9 \times 8 \times 7}{1 \times 2 \times 3 \times 4} \times \frac{8 \times 7 \times 6 \times 5}{1 \times 2 \times 3 \times 4}) + (\frac{10 \times 9 \times 8}{1 \times 2 \times 3} \times \frac{8 \times 7 \times 6}{1 \times 2 \times 3}) + (\frac{10 \times 9}{1 \times 2} \times \frac{8 \times 7}{1 \times 2}) + (10 \times 8) + (1 \times 1)$

= (252 × 56) + (210 × 70) + (120 × 56) + (45 × 28) + 80 + 1

= 14112 + 14700 + 6720 + 1260 + 80 + 1

= 36873

Men in majority :

In a committee of 10 persons if men are in majority, then they are 6 or 7 or 8 in numbers.

∴ the number of committees in which men are in majority

= ⁸C₆ × ¹⁰C₄ + ⁸C₇ × ¹⁰C₃ + ⁸C₈ × ¹⁰C₂

= $\frac{8!}{6! 2!} \times \frac{10!}{4! 6!} + \frac{8!}{7! 1!} \times \frac{10!}{3! 7!} + \frac{8!}{8! 0!} \times \frac{10!}{2! 8!}$

= $(\frac{8 \times 7}{1 \times 2} \times \frac{10 \times 9 \times 8 \times 7}{1 \times 2 \times 3 \times 4}) + (8 \times \frac{10 \times 9 \times 8}{1 \times 2 \times 3}) + (1 \times \frac{10 \times 9}{1 \times 2})$

= (28 × 210) + (8 × 120) + 45

= 5880 + 960 + 45

= 6885

Q.24 A question paper has two sections. section I has 5 questions and section II has 6 questions. A student must answer at least two question from each section among 6 questions he answers. How many different choices does the student have in choosing questions?

There are 11 questions, out of which 5 questions are from section I and 6 questions are from section II.

The student has to select 6 questions taking at least 2 questions from each section.

Consider the following table:

	Case I	Case II	Case III
No. of questions	Sec I (2Q) Sec II (4Q)	Sec I (3Q) Sec II (3Q)	Sec I (4Q) Sec II (2Q)
Number of ways	⁵C₂ × ⁶C₄ = 10 × 15 = 150	⁵C₃ × ⁶C₃ = 10 × 20 = 200	⁵C₄ × ⁶C₂ = 5 × 15 = 75

∴ Number of choices = 150 + 200 + 75 = 425

∴ In 425 ways students can select 6 questions, taking at least 2 questions from each section.

Q.25 There are 3 wicketkeepers and 5 bowlers among 22 cricket players. A team of 11 players is to be selected so that there is exactly one wicketkeeper and at least 4 bowlers in the team. How many different teams can be formed?

Among 22 cricket players there are 3 wicketkeepers + 5 bowlers = 8 players and the remaining (22 – 8) = 14 players are batsmen.

To select 11 players for the team such that it includes exactly 1 wicketkeeper and at least 4 bowlers, the possible selections are,

1 wicketkeeper, 4 bowlers and 6 batsmen.

1 wicketkeeper, 5 bowlers and 5 batsmen.

∴ the number of ways in which a team of 11 players can be chosen

= ³C₁ × ⁵C₄ × ¹⁴C₆ + ³C₁ × ⁵C₅ × ¹⁴C₅

= $3 \times \frac{5!}{4! 1!} \times \frac{14!}{6! 8!} + 3 \times 1 \times \frac{14!}{5! 9!}$

= $3 \times 5 \times \frac{14 \times 13 \times 12 \times 11 \times 10 \times 9}{1 \times 2 \times 3 \times 4 \times 5 \times 6} + 3 \times \frac{14 \times 13 \times 12 \times 11 \times 10}{1 \times 2 \times 3 \times 4 \times 5}$

= (15 × 7 × 13 × 11 × 3) + (3 × 14 × 13 × 11)

= 45045 + 6006

= 51051.

Q.26 Five students are selected from 11. How many ways can these students be selected if :

i. two specified students are selected ?

5 students are to be selected from 11 students

When 2 specified students are included then remaining 3 students can be selected from (11 – 2) = 9 students.

∴ Number of ways of selecting 3 students from 9 students = ⁹C₃

= $\frac{9!}{3! \times 6!}$

= $\frac{9 \times 8 \times 7 \times 6!}{3 \times 2 \times 1 \times 6!}$

= 84

∴ Selection of students is done in 84 ways when 2 specified students are included.

ii. two specified students are not selected ?

Number of students is 11. We have to select 5 students

2 particular students are not selected:

If 2 particular students are not selected, then from remaining (11 – 2) = 9 students, we have to select 5 students.

This can be done in ⁹C₅ ways.

∴ total number of selections

= ⁹C₅

= $\frac{9}{5! 4!}$

= $\frac{9 \times 8 \times 7 \times 6}{1 \times 2 \times 3 \times 4}$

= 126.

Miscellaneous Exercise 3

I II.1 II.2 II.3 II.4 II.5 II.6 II.7 II.8 II.9 II.10 II.11 II.12 II.13 II.14 II.15 II.16 II.17 II.18

I. Select the correct answer from the given alternatives

1. A college offers 5 courses in the morning and 3 in the evening. The number of ways a student can select exactly one course, either in the morning or in the evening

A. 5 B. 3

C. 8 D. 15

Explanation;

Number of ways to select one course from available 8 courses (i.e. 5 courses in the morning and 3 in the evening) = 5 + 3 = 8

2. A college has 7 courses in the morning and 3 in the evening. The possible number of choices with the student if he wants to study one course in the morning and one in the evening is :

A. 21 B. 4

C. 42 D. 10

A. 21

A college has 7 courses in the morning and 3 in the evening.

The possible number of choices with the student if he wants to study one course in the morning and one in the evening is - 21

3. In how many ways can 8 indians, 4 Americans and 4 Englishmen can be seated in a row so that all persons of the same nationality sit together?

A. 3! 8! B. 3! 4! 8! 4!

C. 4! 4! D. 8! 4! 4!

B. 3! 4! 8! 4!

Explanation;

8 Indians take their seats in 8! ways 4

Americans take their seats in 4! ways 4

Englishmen take their seats in 4! Ways.

Three groups of Indians, Americans and Englishmen can be permuted in 3! ways

Required number = 3! × 8! × 4! × 4!

4. In how many ways can 10 examination papers be arranged so that the best and the worst papers never come together?

A. 9 × 8! B. 8 × 8!

C. 9 × 9! D. 8 × 9!

Correct Answer is option D. 8 × 9!

5. In how many ways 4 boys and 3 girls can be seated in a row so that they are alternate.

A. 12 B. 288

C. 144 D. 256

Correct Answer is option C. 144

Explanation;

B G B G B G B

4 boys take their seats in 4! ways

3 girls take their seats in 3! ways

Required number = 4! × 3!

= 24 × 6

= 144

6. Find the number of triangles which can be formed by joining the angular points of a polygon of 8 sides as vertices.

A. 16 B. 56

C. 24 D. 8

Correct Answer is Option B. 56

7. A question paper has two parts, A and B, each containing 10 questions. If a student has to choose 8 from part A and 5 from part B, in how many ways can he choose the question?

A. 320 B. 750

C. 40 D. 11340

Correct Answer is Option D. 11340

Explanation;

Number of ways to choose 8 questions from

Part A and 5 from Part B = ¹⁰C₈ × ¹⁰C₅

= ¹⁰C₂ × ¹⁰C₅

= 45 × 252

= 11340

8. There are 10 persons among whom two are brothers. The total number of ways in which these persons can be seated around a round table so that exactly one person sits between the brothers, is equal to :

A. 2! × 7! B. 2! × 8!

C. 3! × 7! D. 3! × 8!

Correct Answer is Option B. 2! × 8!

Explanation;

Exactly one person sits in between 2 brothers in 8 ways from 8 persons excluding 2 brothers.

The two brothers can change their places in ²P₂ = 2! ways.

After this, the remaining 7 persons can sit in ⁷P₇ = 7! ways.

∴ required number of ways = 8 × 2! × 7! = 2! × 8!

9. The number of arrangement of the letters of the word BANANA in which two N's do not appear adjacently is :

A. 80 B. 60

C. 40 D. 100

Correct Answer is Option C. 40

Explanation;

Arrange B, A, A, A in $\frac{4!}{3!}$ ways.

These four letters create 5 gaps in which 2N are to be filled, this can be done in ⁵C₂ ways, we do not permute those 2N as they are identical.

Required number = $\frac{4!}{3!} \times^{5} C_{2}$ = 40

10. The number of ways in which 5 male and 2 female members of a committee can be seated around a round table so that the two females are not seated together is :

A. 840 B. 600

C. 720 D. 480

Correct Answer is Option D. 480

Explanation;

Required answer = (5 – 1)! × ⁵p₂

II. Answer the following.

1. Find the value of r if ⁵⁶P_r+6 : ⁵⁴P_r+3 = 30800 : 1

⁵⁶P_r+6 : ⁵⁴P_r+3 = 30800 : 1

∴ $\frac{^{56} P_{r + 6}}{^{54} P_{r + 3}} = \frac{30800}{1}$

∴ $\frac{\frac{56!}{(56 - r - 6)!}}{\frac{54!}{(54 - r - 3)!}} = 30800$

∴ $\frac{56!}{(56 - r - 6)!} \times \frac{(54 - r - 3)!}{54!} = 30800$

∴ $\frac{56!}{(50 - r)!} \times \frac{(51 - r)!}{54!} = 30800$

∴ $\frac{56 \times 55 \times 54!}{(50 - r)!} \times \frac{(51 - r) (50 - r)!}{54!} = 30800$

∴ 51 − r = $\frac{30800}{56 \times 55}$

∴ 51 − r = 10

∴ r = 51 − 10

∴ r = 41

2. How many words can be formed by writing letters in the word CROWN in different order?

In the word 'CROWN', the number of letters is n = 6.

∴ the number of all possible words is

n! = 5!

= 5 × 4 × 3 × 2 × 1

= 120.

3. Find the number of words that can be formed by using all the letters in the word REMAIN. If these words are written in dictionary order, what will be the 40^th word?

There are 6 letters A, E, I, M, N, R

Number of words starting with A = 5!

Number of words starting with E = 5!

Number of words starting with I = 5!

Number of words starting with M = 5!

Number of words starting with N = 5!

Number of words starting with R = 5!

Total number of words = 6 × 5! = 720

Number of words starting with AE = 4! = 24

Number of words starting with AIE = 3! = 6

Number of words starting with AIM = 3! = 6

Number of words starting with AINE = 2!

Total words = 24 + 6 + 6 + 2 = 38

39^th word is AINMER

40^th word is AINMRE

4. Capital English alphabet has 11 symmetric letters that appear same when looked at in a mirror. These letters are A, H, I, M, O, T, U, V, W, X and Y. How many symmetric three letters passwords can be formed using these letters?

Total number of symmetric three letters passwords formed from 11 symmetric letters

= ¹¹P₃

= $\frac{11!}{8!}$

= 11 × 10 × 9

= 990

5. How many numbers formed using the digits 3, 2, 0, 4, 3, 2, 3 exceed on million?

A number that exceeds one million is to be formed from the digits 3, 2, 0, 4, 3, 2, 3.

Then the numbers should be any number of 7 digits that can be formed from these digits.

Also among the given numbers 2 is repeated twice and 3 is repeated thrice.

∴ Required number of numbers = Total number of arrangements possible among these digits – number of arrangements of 7 digits which begin with 0.

= $\frac{7!}{2! 3!} - \frac{6!}{2! 3!}$

= $\frac{7 \times 6 \times 5 \times 4 \times 3!}{2 \times 3!} - \frac{6 \times 5 \times 4 \times 3!}{2 \times 3!}$

= 7 × 6 × 5 × 2 – 6 × 5 × 2

= 6 × 5 × 2(7 – 1)

= 60 × 6

= 360

∴ 360 numbers that exceed one million can be formed with the digits 3, 2, 0, 4, 3, 2, 3.

6. Ten students are to be selected for a project from a class of 30 students. There are 4 students who want to be together either in the project or not in the project. Find the number of possible selections.

Case I	Case II
4 Students are in	4 Students are out
Number of ways = ²⁶C₆	Number of ways = ²⁶C₁₀

Required number = ²⁶C₆ + ²⁶C₁₀

= 230230 + 5311735

= 5541965

7. A student finds 7 books of his interest, but can borrow only three books. He wants to borrow Chemistry part II book only if Chemistry part I can also be borrowed. Find the number of ways he can choose three books that he wants to borrow.

There are 7 books of interest and only 3 books can be borrowed.

(i) If Chemistry part-I is selected, then Chemistry part-II is also borrowed. Thus the only a third book is selected from the remaining (7 – 2) = 5 books.

∴ the number of ways of selecting 3 books such that Chemistry part-I is selected

= ⁵C₁

= 5

(ii) If Chemistry part-I is not selected, then Chemistry part-II is not borrowed, therefore, he has to select all 3 books from the remaining (7 – 2) = 5 books.

∴ the number of ways of selecting 3 books such that Chemistry part-I is not selected

= ⁵C₃

= $\frac{5!}{3! 2!}$

= $\frac{5 \times 4}{1 \times 2}$

= 10

Hence, the total number of ways of selecting 3 books to be borrowed

= 5 + 10

= 15

8. 30 Objects are to be divided in three groups containing 7, 10, 13 objects. Find the number of distinct ways for doing so.

Required number = ³⁰C₇ × ²³C₁₀ × ¹³C₁₃

= $\frac{30!}{23! 7!} \times \frac{23!}{10! 13!} \times 1$

= $\frac{30!}{7! 10! 13!}$

9. A student passes an examination if he secures a minimum in each of the 7 subjects. Find the number of ways a student can fail.

A student fail, if he does not secure the minimum marks in either 1, 2, 3, 4, 5, 6 or 7 subjects.

∴ the total number of ways in which a student can fail

= ⁷C₁ + ⁷C₂ + ⁷C₃ + ⁷C₄ + ⁷C₅ + ⁷C₆ + ⁷C₇

= $7 + \frac{7 \times 6}{2 \times 1} + \frac{7 \times 6 \times 5}{3 \times 2 \times 1} + \frac{7 \times 6 \times 5}{3 \times 2 \times 1} + \frac{7 \times 6}{2 \times 1} + 7 + 1$

= 7 + 21 + 35 + 35 + 21 + 7 + 1

= 127

Alternative method:

For each subject, a student has two possible outcomes-to secure minimum marks or he does not.

∴ total number of outcomes for 7 subjects

= 2 × 2 × 2 × ... 7 times

= 2⁷

= 128

Of these there is only one outcome in which he secures the minimum marks in all subjects to pass.

Hence, the number of ways a student can fail

= 128 – 1

= 127

10. Nine friends decide to go for a picnic in two groups. One group decides to go by car and the other group decides to go by train. Find the number of different ways of doing so if there must be at least 3 friends in each group.

	Train	Car	Number of outcomes
No. of friends	3	6	⁹C₃
	4	5	⁹C₄
	5	4	⁹C₅
	6	3	⁹C₆

Required number = ⁹C₃ + ⁹C₄ + ⁹C₅ + ⁹C₆

11. A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.

There are 12 lamps, i.e., n = 12.

Now, if at least one of the switches is 'on' the hall can be illuminated.

∴ the number of ways in which the hall can be illuminated = 2ⁿ – 1

= 2¹²– 1

= 4096 – 1

= 4095

12. How many quadratic equations can be formed using numbers from 0, 2, 4, 5 as coefficients if a coefficient can be repeated in an equation.

Let the quadratic equation be ax² + bx + c = 0, a ≠ 0

Coefficient	Values	Number of ways
a	2, 4, 5	3
b	0, 2, 4, 5	4
c	0, 2, 4, 5	4

Required number = 3 × 4 × 4 = 48

13. How many six-digit telephone numbers can be formed if the first two digit are 45 and no digit can appear more than once?

Digits are 0, 1, 2, ... , 9 i.e., n = 10

The first two digits in each telephone number are 45.

∴ out of six-digit telephone numbers, only 4 digits from the remaining (10 – 2) = 8 digits are to be arranged.

Hence, the number of ways in which 6-digit telephone numbers can be formed

= ⁸P₄

= 8 × 7 × 6 × 5

= 1680

14. A question paper has 6 questions. How many ways does a student have to answer if he wants to solve at least one question?

Every question is ‘SOLVED’ or ‘NOT SOLVED’

There are 6 question.

Number of outcomes = 2⁶

This number includes the case when the student solves NONE of the question.

Required number = 2⁶ – 1

= 64 – 1

= 63

15. Find the number of ways of dividing 20 objects in three groups of sizes 8, 7 and 5.

Required number = ²⁰C₈ × ¹²C₇ × ⁵C₅

= $\frac{20!}{8! 12!} \times \frac{12!}{7! 5!} \times 1$

= $\frac{20!}{8! 7! 5!}$

16. There are 4 doctors and 8 lawyers in a panel. Find the number of ways for selecting a team of 6 if at least one doctor must be in the team.

We count the number by INDIRECT method of counting.

Number of ways to select a team of 6 people = ¹²C₆

Number of teams with No doctor in any team = ⁸C₆

Required number = ¹²C₆ – ⁸C₆

= 924 – 28

= 896

17. Four parallel lines intersect another set of five parallel lines. Find the number of distinct parallelograms formed.

To form a parallelogram, we have to select any 2 of 4 parallel lines and any 2 of another 5 parallel lines for intersecting.

∴ the number of parallelograms which can be formed

= ⁴C₂ × ⁵C₂

= $\frac{4!}{2! 2!} \times \frac{5!}{2! 3!}$

= ⁵P₅

= $\frac{4 \times 3}{2 \times 1} \times \frac{5 \times 4}{2 \times 1}$

= 6 × 10

= 60.

18. There are 12 distinct points A, B, C, ...., L in order, on a circle. Lines are drawn passing through each pair of points.

i. How many lines are there in total?

ii. How many lines pass through D?

iii. How many triangles are determined by lines?

iv. How many triangles have on vertex C?

i. Total Number of lines = ¹²C₂= 66

ii. Lines through D will pass through any one of the remaining 11 points.

∴ the total number of lines pass through D = 11.

iii. We need three points to draw a triangle.

Number of triangles = ¹²C₃ = 220

iv. If one of the vertices of the triangle is on C, then the other two vertices can be chosen from the remaining 11 points.

This can be done in ¹¹C₂ ways.

∴ the total number of triangles have vertex on C

= ¹¹C₂

= $\frac{11!}{2! 9!}$

= $\frac{11 \times 10}{1 \times 2}$

= 55

Mathematics Part - II

Chapter No. 03 - Permutation and Combination

Exercise 3.1

Q.1 A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl or a boy?

There are 30 boys and 20 girls.

A teacher can select any boy as a class monitor from 30 boys in 30 different ways and he can select any girl as a class monitor from 20 girls in 20 different ways.

∴ by the fundamental principle of addition, the total number of ways a teacher can select a class monitor

= 30 + 20 = 50

Hence, there are 50 different ways to select a class monitor.

Q.2 A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?

A signal is generated from 2 flags and there are 4 flags of different colours available.

∴ 1st flag can be any one of the available 4 flags.

∴ It can be selected in 4 ways.

Now, 2nd flag is to be selected for which 3 flags are available for a different signal.

∴ 2nd flag can be anyone from these 3 flags.

∴ It can be selected in 3 ways.

∴ By using fundamental principle of multiplication, total no. of ways a signal can be generated

= 4 × 3

= 12

∴ 12 different signals can be generated.

Q.3 How many two letter words can be formed using letters from the word SPACE, when repetition of letters

i. is allowed ?

Number of letters in the word 'SPACE' = 5

In 2-lettered words, both the letters can be selected in 5 different ways, if repetitions of the letters are allowed.

∴ by fundamental principle of multiplication, the total number of 2-lettered words

= 5 × 5

= 25

ii. is not allowed ?

Two-letter word is to be formed out of the letters of the word SPACE.

When repetition of the letters is not allowed

1st letter can be selected in 5 ways

2nd letter can be selected in 4 ways

∴ By using fundamental principle of multiplication, total number of 2-letter words

= 5 × 4

= 20

Q.4 How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits

i. is allowed ?

A 3-digit number has 3 places which from left to right are hundred's place, ten's place, and unit's place.

Zero cannot be in the hundred's place. Hence, hundred's place can be filled in by anyone of the 4 non-zero digits 1, 3, 5, 6. Thus hundred's places can be filled in 4 ways.

Since repetition of digits is allowed, the ten's place and unit's place can be filled by anyone of the given 5 digits i.e., ten's place and unit's place can be filled in 5 different ways each.

∴ by fundamental principle of multiplication, the total number of 3-digit numbers formed

= 4 × 5 × 5

= 100

ii. is not allowed ?

Three-digit number is to be formed from the digits 0, 1, 3, 5, 6

When repetition of digits is not allowed 100’s place digit should be a non zero number.

Hence, it can be any one from digits 1, 3, 5, 6

∴ 100’s place digit can be selected in 4 ways

10’s and unit’s place digit can be zero

But digits can’t be repeated

∴ 10’s place digit can be selected in 4 ways and unit’s place digit can be selected in 3 ways

∴ By using fundamental principle of multiplication, total number of two-digit numbers

= 4 × 4 × 3

= 48

Q.5 How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?

A 3-digit number has three places which from left to right are hundred's place, ten's place and unit's place.

Here we have to form 3-digit numbers using the digits 2, 3, 4, 5, 6.

The hundred's place can be filled in by using any one of the given 5 digits in 5 ways.

Since, repetition of digits is allowed each ten's place and unit's place can be filled in by any one of the given 5 digits in 5 ways.

∴ by fundamental principle of multiplication, the total number of 3-digit numbers

= 5 × 5 × 5

= 125.

Q.6 A letter lock contains 3 rings, each ring containing 5 different letters. Determine the maximum number of false trials that can be made before the lock is opened?

Since there are 3 rings each containing 5 different letters.

∴ each ring can be adjusted in 5 different ways,

i.e., m = 5, n = 5, p = 5

∴ by the fundamental principle, 3 rings can be arranged in

= m × n × p

= 5 × 5 × 5

= 125 ways

Out of these 125 trials only one trial is successful to open the lock.

Hence, the maximum number of false trials

= 125 − 1

= 124

Q.7 In a test, 5 questions are of the form 'state, true or false'. No student has got all answers correct. Also, the answer of every student is different. Find the number of students appeared for the test.

True/false questions can be answered in 2 ways either by making it true or false.

∴ each of the 5 questions can be answered in 2 different ways.

∴ total number of different sequences of answers

25 = 2 × 2 × 2 × 2 × 2 = 32

Out of these one sequence is of correct answers and no student has written all correct answers.

∴ 1^st flag can be any one of the available 4 flags.

Now, 2^nd flag is to be selected for which 3 flags are available for a different signal.

∴ 2^nd flag can be anyone from these 3 flags.

1^st letter can be selected in 5 ways

2^nd letter can be selected in 4 ways

2⁵ = 2 × 2 × 2 × 2 × 2 = 32