Correct answer is (A)
For temperature maximum p-v product
should be
maximum
=
0
at v =
T = 0
Option (a)
11. (JEE Main 2021 (Online) 31st August Morning Shift )
For an ideal gas the instantaneous change in pressure 'p' with volume 'v' is given by the equation . If p = p0 at v =0 is the given boundary condition, then the maximum temperature one mole of gas can attain is : (Here R is the gas constant)
(A)
(B)
(C) infinity
(D) 0C
Correct answer is (A)
For temperature maximum p-v product
should be
maximum
=
0
at v =
T = 0
Option (a)
12. (JEE Main 2021 (Online) 27th August Morning Shift )
A balloon carries a total load of 185 kg at normal pressure and temperature of 27C. What load will the balloon carry on rising to a height at which the barometric pressure is 45 cm of Hg and the temperature is 7C. Assuming the volume constant?
(A) 181.46 kg
(B) 214.15 kg
(C) 219.07 kg
(D) 123.54 kg
Correct answer is (D)
Pm =
RT
kg
13. (JEE Main 2021 (Online) 26th August Evening Shift )
A cylindrical container of volume 4.0
103 m3 contains one mole of hydrogen and
two
moles of carbon dioxide. Assume the temperature of the mixture is 400 K. The pressure of the mixture of
gases is :
[Take gas constant as 8.3 J
mol1
K1]
(A) 249 101 Pa
(B) 24.9 103 Pa
(C) 24.9 105 Pa
(D) 24.9 Pa
Correct answer is (C)
V = 4
103 m3
n = 3
moles
T
= 400 K
PV = nRT
P =
P =
= 24.9
105 Pa
14. (JEE Main 2021 (Online) 20th July Evening Shift )
Which of the following graphs represent the behavior of an ideal gas? Symbols have their usual meaning.
(A) 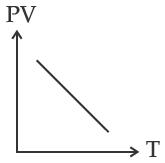
(B) 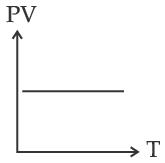
(C) 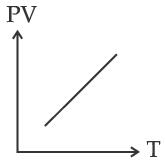
(D) 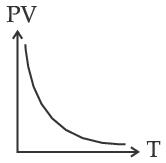
Correct answer is (C)
PV = nRT
PV
T
Straight line with positive slope (nR)
15. (JEE Main 2021 (Online) 16th March Morning Shift )
The volume V of an enclosure contains a mixture of three gases, 16 g of oxygen, 28 g of nitrogen and 44 g of carbon dioxide at absolute temperature T. Consider R as universal gas constant. The pressure of the mixture of gases is :
(A)
(B)
(C)
(D)
Correct answer is (D)
No. of moles of O2 :
n1 =
= 0.5 mole
No. of moles of N2
:
n2 =
= 1 mole
No. of moles of CO2 :
n3 =
= 1 mole
Total no. of moles in container
: n
= n1 + n2 +
n3
n = 0.5 + 1 + 1 =
moles
Now; PV =
nRT
P =
P =