1. ⇒ (MHT CET 2023 13th May Morning Shift )

A body of mass $0.04 kg$ executes simple harmonic motion (SHM) about $x = 0$ under the influence of force $F$ as shown in graph. The period of

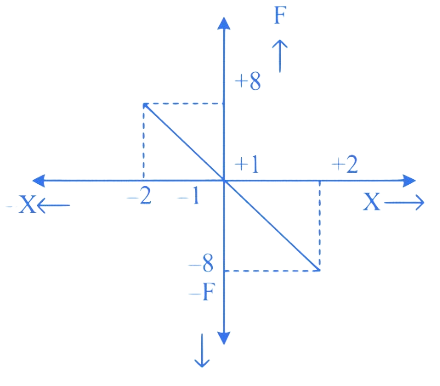
A. $2 π s$

B. $0.2 π s$

C. $π d$

D. $\frac{π}{2} s$

Correct Option is (B)

$\begin{aligned} k = 400 N / m \\ m = 0.04 \end{aligned}$

From the graph,

$K = \frac{F}{x} = \frac{8}{2} = 4$

From $T = 2 π \sqrt{\frac{M}{K}}$ ,

we get

$T = 2 π \sqrt{\frac{0.04}{4}} = 0.2 π s$

2. ⇒ (MHT CET 2023 10th May Evening Shift )

A simple harmonic progressive wave is represented by $y = A \sin (100 π t + 3 x)$ . The distance between two points on the wave at a phase difference of $\frac{π}{3}$ radian is

A. $\frac{π}{8} m$

B. $\frac{π}{9} m$

C. $\frac{π}{6} m$

D. $\frac{π}{3} m$

Correct Option is (B)

Equation of the given harmonic progressive wave $y = A \sin (100 π t + 3)$ ...... (i)

General equation of a harmonic wave

$y = A \sin (wt + kx)$ ..... (ii)

From equations (i) and (ii), $ω = 100 π, k = 3$

But, $k = \frac{2 π}{λ} \Rightarrow 3 = \frac{2 π}{λ}$

$∴ λ = \frac{2 π}{3}$

We also know,

Path difference $Δ x = \frac{λ}{2 π} \times$ Phase difference $Δ ϕ$

$\begin{aligned} ∴ Δ x & = \frac{2 π}{3 \times 2 π} \times \frac{π}{3} \dots . (Given Δ ϕ = \frac{π}{3}) \\ = \frac{π}{9} m \end{aligned}$

3. ⇒ (MHT CET 2023 9th May Evening Shift )

Two S.H.Ms. are represented by equations $y_{1} = 0.1 \sin (100 π t + \frac{π}{3})$ and $y_{2} = 0.1 \cos (100 π t)$ The phase difference between the speeds of the two particles is

A. $\frac{π}{3}$

B. $- \frac{π}{6}$

C. $+ \frac{π}{6}$

D. $- \frac{π}{3}$

Correct Option is (B)

Given: $y_{1} = 0.1 \sin (100 π t + \frac{π}{3})$ and

$\begin{aligned} y_{2} = 0.1 \cos (100 π t) \\ ∴ v_{1} = \frac{{dy}_{1}}{dt} & = 0.1 \times 100 π \cos (100 π t + \frac{π}{3}) \\ v_{2} = \frac{{dy}_{2}}{dt} & = - 0.1 \times 100 π \sin (100 π t) \\ = (0.1 \times 100 π) \cos (100 π t + \frac{π}{2}) \end{aligned}$

Phase difference of velocity of first particle with respect to the velocity of second particle at $t = 0$ is

$∴ Δ ϕ = ϕ_{1} - ϕ_{2} = \frac{π}{3} - \frac{π}{2} = \frac{- π}{6}$

4. ⇒ (MHT CET 2023 9th May Morning Shift )

The maximum velocity of a particle performing S.H.M. is ' $V$ '. If the periodic time is made ${(\frac{1}{3})}^{d}$ and the amplitude is doubled, then the new maximum velocity of the particle will be

A. $\frac{V}{6}$

B. $\frac{3 V}{2}$

C. $3 V$

D. $6 V$

Correct Option is (D)

Given $T^{'} = \frac{1}{3} T$ and $A^{'} = 2 A$

$∴ ω^{'} = \frac{2 π}{T^{'}} = \frac{2 π}{(\frac{1}{3} T)} = \frac{6 π}{T} = 3 ω$

$\begin{aligned} ∴ The new maximum velocity \\ \begin{aligned} V^{'} & = A^{'} ω^{'} \\ = (2 A) \times (3 ω) \\ = 6 A ω \\ = 6 V \end{aligned} \end{aligned}$

5. ⇒ (MHT CET 2021 21th September Evening Shift )

A particle is performing S.H.M. with maximum velocity ' $v$ '. If the amplitude is tripled and periodic time is doubled then maximum velocity will be

A. $1.5 v$

B. $3 v$

C. $2 v$

D. $v$

Correct Option is (A)

$V = V_{\max} = ω A = \frac{2 π}{T} . A$

If A is tripled and T is doubled, $V_{\max}$ will become $\frac{3}{2}$ times or 1.5 times.

⇒Oscillations