1. ⇒ (MHT CET 2023 12th May Evening Shift )

A thin wire of length ' $L$ ' and uniform linear mass density ' $m$ ' is bent into a circular coil. The moment of inertia of this coil about tangential axis and in plane of the coil is

A. $\frac{3 {mL}^{2}}{5 π^{2}}$

B. $\frac{3 {mL}^{3}}{8 π^{2}}$

C. $\frac{3 {mL}^{3}}{4 π^{2}}$

D. $\frac{3 {mL}^{2}}{7 π^{2}}$

Correct Option is (B)

$∴$ Moment of inertia of thin wire:

$\begin{aligned} I & = \frac{M^{2}}{2} \\ M & = v \times m and L = 2 π R \\ R & = \frac{L}{2 π} \\ ∴ I & = \frac{L m}{2} {(\frac{L}{2 π})}^{2} \\ I & = \frac{m L^{3}}{8 π^{2}} \end{aligned}$

$∴$ Using Parallel axis theorem:

$\begin{aligned} I^{'} = I + M R^{2} \\ I = \frac{m L^{3}}{8 π^{2}} + L m {(\frac{L}{2 π})}^{2} \\ I = \frac{3 m L^{3}}{8 π^{2}} \end{aligned}$

2. ⇒ (MHT CET 2023 12th May Morning Shift )

$I_{1}$ is the moment of inertia of a circular disc about an axis passing through its centre and perpendicular to the plane of disc. $I_{2}$ is its moment of inertia about an axis $A B$ perpendicular to plane and parallel to axis $CM$ at a distance $\frac{2 R}{3}$ from centre. The ratio of $I_{1}$ and $I_{2}$ is $x : 17$ . The value of ' $x$ ' is (R = radius of the disc)

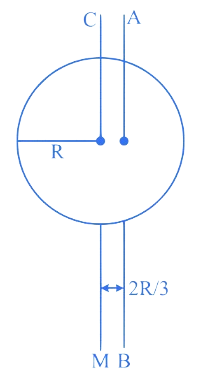
MHT CET 2023 12th May Morning Shift Physics - Rotational Motion Question 5 English

A. 9

B. 12

C. 15

D. 17

Correct Option is (A)

Using Parallel axis theorem, $I_{2} = I_{1} + {Mh}^{2}$

For a disc, $I_{1} = \frac{1}{2} M R^{2}$ and given that, $h = \frac{2 R}{3}$

$\begin{aligned} ∴ I_{2} = \frac{1}{2} {MR}^{2} + M (\frac{4 R^{2}}{9}) \\ ∴ I_{2} = \frac{1}{2} {MR}^{2} (1 + \frac{8}{9}) = I_{1} \times \frac{17}{9} \\ ∴ \frac{I_{1}}{I_{2}} = \frac{9}{17} \end{aligned}$

3. ⇒ (MHT CET 2023 11th May Evening Shift )

From a disc of mass ' $M$ ' and radius ' $R$ ', a circular hole of diameter ' $R$ ' is cut whose rim passes through the centre. The moment of inertia of the remaining part of the disc about perpendicular axis passing through the centre is

A. $\frac{13 {MR}^{2}}{32}$

B. $\frac{11 {MR}^{2}}{32}$

C. $\frac{9 {MR}^{2}}{32}$

D. $\frac{7 {MR}^{2}}{32}$

Correct Option is (A)

MHT CET 2023 11th May Evening Shift Physics - Rotational Motion Question 16 English Explanation

Moment of inertia of disc is given by

$I_{disc} = I_{r} + I_{hole}$ $\dots . {I_{r} =$ M.I. of remaining part $}$

$∴ I_{r} = I_{disc} - I_{hole}$ ..... (i)

$I_{disc} = \frac{{MR}^{2}}{2}$ ..... (ii)

By parallel axes theorem we get,

$I_{hole} = [\frac{\frac{M}{4} {(\frac{R}{2})}^{2}}{2} + \frac{M}{4} {(\frac{R}{2})}^{2}]$

$\dots . {\begin{cases} ∵ M_{hole} = \frac{M_{dise}}{4} \\ ∵ the surface density is same \end{cases}}$

$∴ I_{hole} = [\frac{{MR}^{2}}{32} + \frac{{MR}^{2}}{16}]$ ..... (iii)

Substituting eq (iii) and eq (ii) in eq (i) we get,

$\begin{aligned} I_{r} & = \frac{{MR}^{2}}{2} - \frac{{MR}^{2}}{32} - \frac{{MR}^{2}}{16} \\ = {MR}^{2} [\frac{1}{2} - \frac{1}{32} - \frac{1}{16}] \\ = \frac{13}{32} {MR}^{2} \end{aligned}$

4. ⇒ (MHT CET 2023 11th May Morning Shift )

Radius of gyration of a thin uniform circular disc about the axis passing through its centre and perpendicular to its plane is $K_{c}$ . Radius of gyration of the same disc about a diameter of the disc is $K_{d}$ . The ratio $K_{c} : K_{d}$ is

A. $\sqrt{2} : 1$

B. $1 : \sqrt{2}$

C. $2 : 1$

D. $1 : 4$

Correct Option is (A)

Let the radius of the disc be $R$

$\begin{aligned} ∴ K_{c} = \frac{R}{\sqrt{2}} \\ ∴ K_{d} = \frac{R}{2} \end{aligned}$

Taking the ratio,

$∴ \frac{K_{c}}{K_{d}} = \frac{\frac{R}{\sqrt{2}}}{\frac{R}{2}} = \frac{\sqrt{2}}{1}$

5. ⇒ (MHT CET 2023 10th May Evening Shift )

What is the moment of inertia of the electron moving in second Bohr orbit of hydrogen atom? [ $h =$ Planck's constant, $m =$ mass of electron, $ε_{0} =$ permittivity of free space, $e =$ charge on electron]

A. $\frac{4 ε_{0}^{2} h^{4}}{π^{2} m e^{4}}$

B. $\frac{8 m ε_{0}^{2} h^{4}}{π^{2} e^{4}}$

C. $\frac{16 ε_{0}^{2} h^{4}}{π^{2} m e^{4}}$

D. $\frac{ε_{0}^{2} h^{4}}{16 π^{2} {me}^{4}}$

Correct Option is (C)

Moment of Inertia $I = {MR}^{2}$

Radius of the $n^{th}$ Bohr orbit is,

$r_{n} = \frac{ε_{0} h^{2} n^{2}}{π {me}^{2}}$

For $n = 2$ ,

$r_{2} = \frac{4 ε_{0} h^{2}}{π {me}^{2}}$

$∴$ Moment of inertia of the electron in the $2^{nd}$ orbit is

$\begin{aligned} M.I & = m \times {[\frac{4 ε_{0} h^{2}}{π m e^{2}}]}^{2} \\ = m \times \frac{16 ε_{0}^{2} h^{4}}{π^{2} m^{2} e^{4}} \\ = \frac{16 ε_{0}^{2} h^{4}}{π^{2} m e^{4}} \end{aligned}$

⇒Rotational Dynamics