1. ⇒ (MHT CET 2023 12th May Evening Shift )

The area (in sq. units) of the smaller part of the circle $x^{2} + y^{2} = a^{2}$ cut off by the line $x = \frac{a}{\sqrt{2}}$ is

A. $\frac{a^{2}}{4} | \frac{π}{2} - 1 |$

B. $a^{2} | \frac{π}{4} - 1 |$

C. $\frac{a^{2}}{2} | \frac{π}{2} - 1 |$

D. $\frac{a^{2}}{4} | \frac{π}{4} - 1 |$

Correct Option is (C)

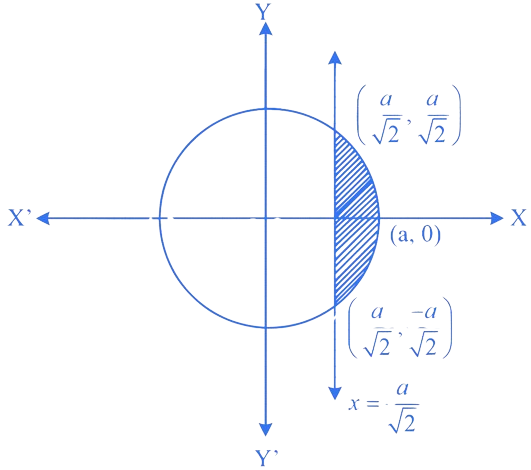
MHT CET 2023 12th May Evening Shift Mathematics - Area Under The Curves Question 2 English Explanation

Substitute $x = \frac{a}{\sqrt{2}}$ in $x^{2} + y^{2} = a^{2}$ , we get $\frac{a^{2}}{2} + y^{2} = a^{2} \Rightarrow y = \pm \frac{a}{\sqrt{2}}$

$∴$ Required area

$\begin{aligned} = 2 \int_{\frac{a}{\sqrt{2}}}^{a} \sqrt{a^{2} - x^{2}} d x \\ = 2 {[\frac{x}{2} \sqrt{a^{2} - x^{2}} + \frac{a^{2}}{2} \sin^{- 1} (\frac{x}{a})]}_{\frac{a}{\sqrt{2}}}^{2} \\ = 2 {[0 + \frac{a^{2}}{2} \times \frac{π}{2}] - [\frac{a}{2 \sqrt{2}} \sqrt{a^{2} - \frac{a^{2}}{2}} + \frac{a^{2}}{2} \times \frac{π}{4}]} \\ = 2 [\frac{a^{2} π}{4} - \frac{a^{2}}{4} - \frac{a^{2} π}{8}] \\ = \frac{a^{2}}{2} | π - 1 - \frac{π}{2} | \\ = \frac{a^{2}}{2} | \frac{π}{2} - 1 | \end{aligned}$

2. ⇒ (MHT CET 2023 12th May Morning Shift )

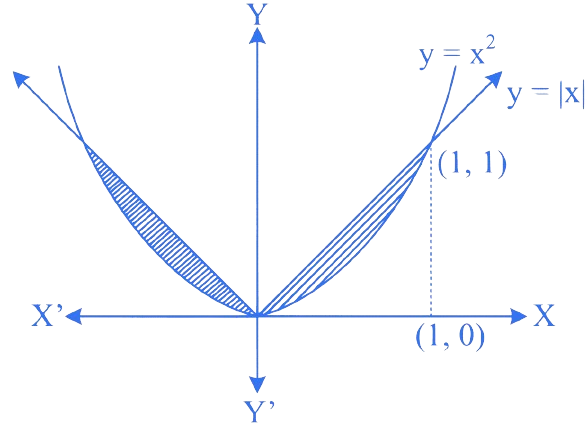
The area of the region bounded by the curves $y = e^{x}, y = \log x$ and lines $x = 1, x = 2$ is

A. $(e - 1)^{2}$ sq. units

B. $(e^{2} - e + 1)$ sq. units

C. $(e^{2} - e + 1 - 2 \log 2)$ sq. units

D. $(e^{2} + e - 2 \log 2)$ sq. units

Correct Option is (C)

Required Area

$\begin{aligned} = \int_{1}^{2} (e^{x} - \log x) d x \\ = {[e^{x}]}_{1}^{2} - \int_{1}^{2} 1 \log x d x \\ = (e^{2} - e) - [x \log x - \int_{1}^{2} 1 d x] \\ = (e^{2} - e) - [x \log x - x]_{1}^{2} \\ = (e^{2} - e) - [(2 \log 2 - 2) - (1 \log 1 - 1)] \\ = e^{2} - e - (2 \log 2 - 2 - 0 + 1) \\ = e^{2} - e - (2 \log 2 - 1) \\ = (e^{2} - e + 1 - 2 \log 2) sq. units \end{aligned}$

3. ⇒ (MHT CET 2023 11th May Morning Shift )

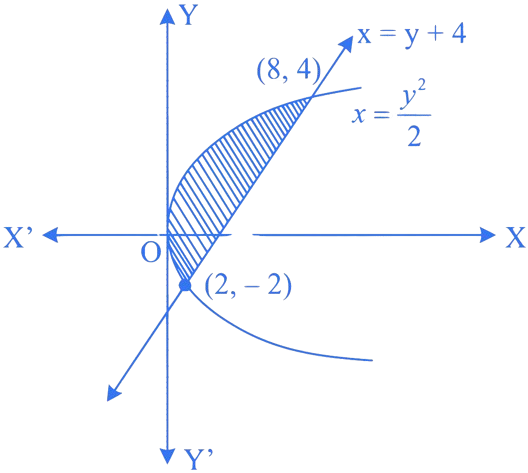
The area of the region bounded by the parabola $y = x^{2}$ and the curve $y = | x |$ is

A. $\frac{1}{2}$ sq. units

B. $\frac{1}{3}$ sq. units

C. $\frac{1}{4}$ sq. units

D. $\frac{1}{6}$ sq. units

Correct Option is (B)

MHT CET 2023 11th May Morning Shift Mathematics - Area Under The Curves Question 4 English Explanation

$\begin{aligned} Required area & = 2 \int_{0}^{1} (x - x^{2}) d x \\ = 2 {[\frac{x^{2}}{2} - \frac{x^{3}}{3}]}_{0}^{1} \\ = 2 (\frac{1}{2} - \frac{1}{3}) = \frac{1}{3} sq.units \end{aligned}$

4. ⇒ (MHT CET 2023 9th May Morning Shift )

The area (in sq. units) of the region $A = {(x, y) / \frac{y^{2}}{2} \leq x \leq y + 4}$ is

A. 30

B. $\frac{53}{3}$

C. 16

D. 18

Correct Option is (D)

Given that $\frac{y^{2}}{2} \leq x \leq y + 4$

$\begin{array}{ll} ∴ & x = \frac{y^{2}}{2} and x = y + 4 \\ \frac{y^{2}}{2} = y + 4^{2} \\ ∴ & y^{2} - 2 y - 8 = 0 \\ ∴ & y = 4 or - 2 \\ \Rightarrow x = 8 or 2 \end{array}$

MHT CET 2023 9th May Morning Shift Mathematics - Area Under The Curves Question 8 English Explanation

$∴ A = \int_{- 2}^{4} (y + 4 - \frac{y^{2}}{2}) d y$

$\begin{aligned} ∴ A = {[\frac{y^{2}}{2} + 4 y - \frac{y^{3}}{6}]}_{- 2}^{4} \\ ∴ A = (8 + 16 - \frac{64}{6}) - (2 - 8 + \frac{8}{6}) \\ ∴ A = 18 \end{aligned}$

5. ⇒ (MHT CET 2021 21th September Morning Shift )

The area of the region bounded by the curve y $^{2}$ = 4x and the line y = x is

A. $\frac{8}{3}$ sq. units

B. $\frac{5}{8}$ sq. units

C. $\frac{3}{8}$ sq. units

D. $\frac{3}{5}$ sq. units

Correct Option is (A)

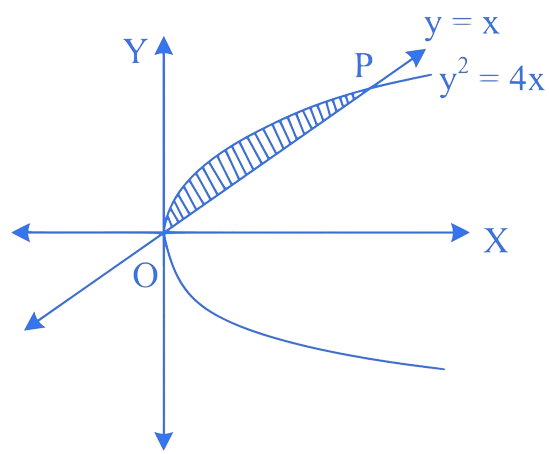
MHT CET 2021 21th September Morning Shift Mathematics - Area Under The Curves Question 11 English Explanation

Refer figure. Point of intersection of given curves $x^{2} = 4 x \Rightarrow x (x - 4) = 0$

$∴ 0 \equiv (0, 0) and P \equiv (4, 4)$

Required area is shaded.

$\begin{aligned} ∴ A & = \int_{0}^{4} (\sqrt{4 x} - x) d x = 2 \int_{0}^{4} x^{\frac{1}{2}} d x - \int_{θ}^{4} x d x \\ = 2 {[\frac{x^{\frac{3}{2}}}{(\frac{3}{2})}]}_{0}^{4} - {[\frac{x^{2}}{2}]}_{0}^{4} = (\frac{4}{3}) (4 \times 2) - \frac{16}{2} \\ = \frac{32}{3} - \frac{16}{2} = \frac{16}{6} = \frac{8}{3} sq. units. \end{aligned}$

⇒Application of Definite Integration