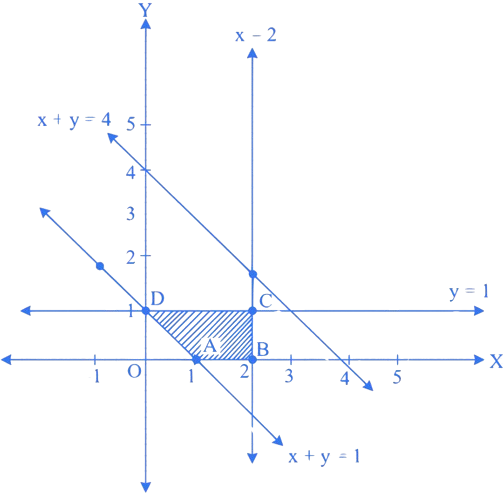
6. ⇒ (MHT CET 2023 10th May Morning Shift )

The vertices of the feasible region for the constraints $x + y \leq 4, x \leq 2, y \leq 1, x + y \geq 1, x, y \geq 0$ are

A. $(1, 0), (2, 0), (2, 1), (0, 4)$

B. $(0, 1), (4, 0), (0, 4), (1, 0)$

C. $(1, 0), (2, 0), (2, 1), (0, 1)$

D. $(1, 0), (4, 0), (2, 1), (0, 4)$

Correct answer option is (C)

Feasible region lies on origin side of $x + y = 4, x = 2, y = 1$ and non-origin side of $x + y = 1$ and in first quadrant.

$∴$ Vertices of feasible region are $A (1, 0), B (2, 0), C (2, 1), D (0, 1)$

MHT CET 2023 10th May Morning Shift Mathematics - Linear Programming Question 4 English Explanation

7. ⇒ (MHT CET 2023 9th May Evening Shift )

The graphical solution set for the system of inequations $x - 2 y \leq 2, 5 x + 2 y \geq 10, 4 x + 5 y \leq 20, x \geq 0, y \geq 0$ is given by

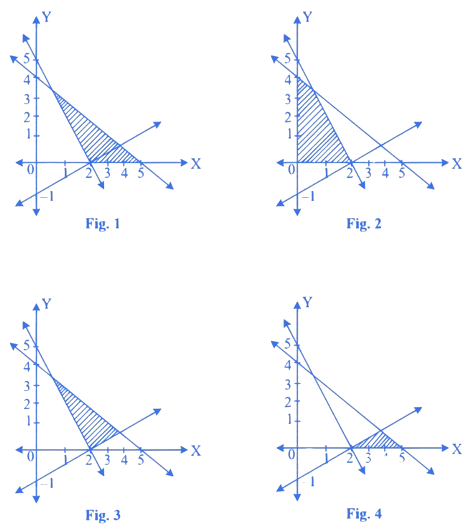
MHT CET 2023 9th May Evening Shift Mathematics - Linear Programming Question 7 English

A. Fig. 2

B. Fig. 4

C. Fig. 1

D. Fig. 3

Correct answer option is (D)

Feasible region lies on origin side of $x - 2 y = 2, 4 x + 5 y = 20$ and on non-origin side of $5 x + 2 y = 10$ , in $1^{st}$ quadrant.

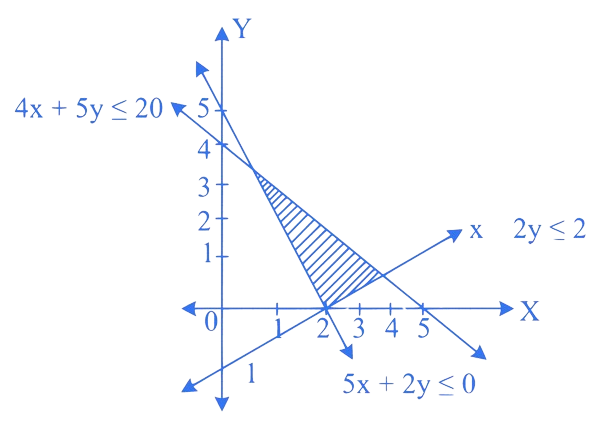
MHT CET 2023 9th May Evening Shift Mathematics - Linear Programming Question 7 English Explanation

8. ⇒ (MHT CET 2023 9th May Morning Shift )

If feasible region is as shown in the figure, then the related inequalities are

MHT CET 2023 9th May Morning Shift Mathematics - Linear Programming Question 8 English

A. $3 x + 4 y \geq 12, y - x \geq 0, y \leq 3, x, y \geq 0$

B. $3 x + 4 y \leq 12, y - x \leq 0, y \geq 3, x, y \geq 0$

C. $3 x + 4 y \leq 12, y - x \geq 0, y \leq 3, x, y \geq 0$

D. $3 x + 4 y \geq 12, y - x \leq 0, y \geq 3, x, y \geq 0$

Correct answer option is (A)

The shaded region lies:

on non-origin side of line $3 x + 4 y = 12$ i.e., $3 x + 4 y \geq 12$ ,

on the side of the line $y - x = 0$ , where $y \geq x$ i.e., $y - x \geq 0$ ,

on origin side of line $y = 3$ i.e., $y \leq 3$ ,

and in first quadrant i.e., $x \geq 0, y \geq 0$ .

9. ⇒ (MHT CET 2021 21th September Evening Shift )

The objective function $z = 4 x + 5 y$ subjective to $2 x + y \geq 7; 2 x + 3 y \leq 15; y \leq 3, x \geq 0; y \geq 0$ has minimum value at the point.

A. on the line $2 x + 3 y = 15$

B. on X-axis

C. on Y-axis

D. origin

Correct answer option is (B)

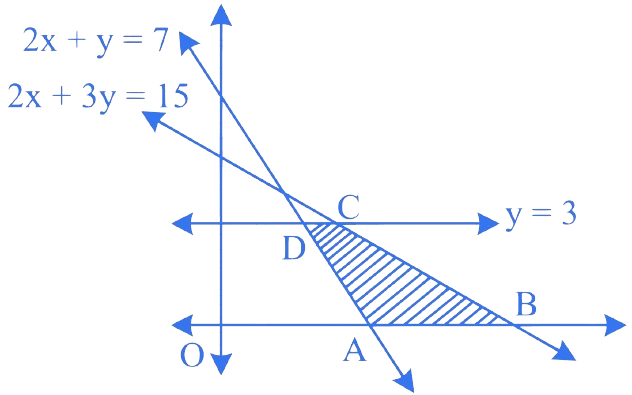
MHT CET 2021 21th September Evening Shift Mathematics - Linear Programming Question 9 English Explanation

We have lines $2 x + y = 7, 2 x + 3 y = 15, y = 3$ Refer figure

The required region is shaded.

We have $A \equiv (\frac{7}{2}, 0), B \equiv (\frac{15}{2}, 0)$

Point of intersection of $2 x + y = 7$ and $y = 3 is D \equiv (2, 3)$

Point of intersection of $2 x + 3 y = 15$ and $y = 3$ is $C \equiv (3, 3)$ We have objective function $z = 4 x + 5 y$

$\begin{aligned} ∴ z_{(A)} & = 4 (\frac{7}{2}) + 5 (0) = 14 + 0 = 14 \\ z_{(B)} & = 4 (\frac{15}{2}) + 5 (0) = 30 + 0 = 30 \\ z_{(C)} & = 4 (3) + 5 (3) = 12 + 15 = 27 \\ z_{(D)} & = 4 (2) + 5 (3) = 8 + 15 = 23 \end{aligned}$

Hence minimum value occurs at point A which lies on X axis.

10. ⇒ (MHT CET 2021 21th September Morning Shift )

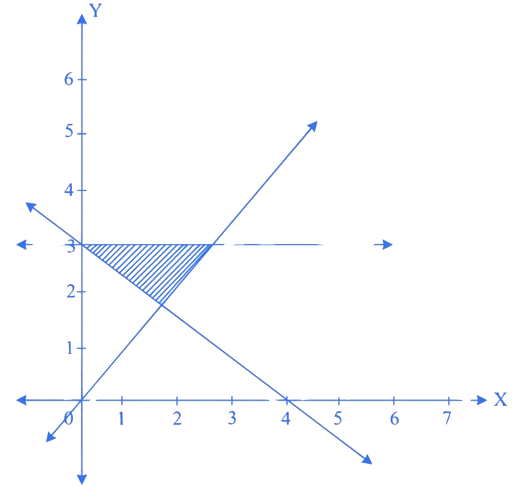
The shaded figure given below is the solution set for the linear inequations. Choose the correct option.

MHT CET 2021 21th September Morning Shift Mathematics - Linear Programming Question 10 English

A. $3 x + 4 y \geq 18; x - 6 y \leq 3; 2 x + 3 y \geq 3; 7 x - 14 y \leq 14; x \geq 0; y \geq 0$

B. $3 x + 4 y \leq 18; x - 6 y \leq 3; 2 x + 3 y \leq 3; - 7 x + 14 y \geq 14; x \geq 0; y \geq 0$

C. $3 x + 4 y \leq 18; x - 6 y \leq 3; 2 x + 3 y \geq 3; - 7 x + 14 y \leq 14; x \geq 0; y \geq 0$

D. $3 x + 4 y \geq - 18; x - 6 y \leq 3; 2 x + 3 y \leq 3; - 7 x + 14 y \geq 14; x \geq 0; y \geq 0$

Correct answer option is (C)

For the shaded region, inequalities are as follows.

$x \geq 0, y \geq 0, 2 x + 3 y \geq 3, x - 6 y \leq 3, 3 x + 4 y \leq 18, - 7 x + 14 y \leq 14$ .

Note:

$- 7 x + 14 y = 14 \Rightarrow 7 x - 14 = - 14 and 0 > - 14$

⇒Linear programming