Correct Answer is Option (A)
F = Kx
10 = K 0.05
K =
= .628 s
1. ⇒ (NEET 2021)
A spring is stretched by 5 cm by a force 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is -
A. 0.628 s
B. 0.0628 s
C. 6.28 s
D. 3.14 s
2. ⇒ (NEET 2017)
A spring of force constant k is cut into lengths of ratio 1 : 2 : 3. They are connected in series and the new force constant is K'. Then they are connected in parallel and force constant is k''. Then k' : k'' is
A. 1 : 9
B. 1 : 11
C. 1 : 14
D. 1 : 6
3. ⇒ (NEET 2016 Phase 2)
A body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg, the time period of oscillations becomes 5 s. The value of m in kg is
A.
B.
C.
D.
4. ⇒ (AIPMT 2010 Prelims)
The period of oscillation of a mass M suspended from a strong of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
A. T
B.
C. 2T
D.
5. ⇒ (AIPMT 2007)
A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the
figure. The mass of the spring and the pan is negligible.
When pressed slightly and released the mass executes a simple harmonic motion. The spring
constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached
from the pan (take g = 10 m/s2).

A. 10.0 cm
B. any value less than 12.0 cm
C. 4.0 cm
D. 8.0 cm
6. ⇒ ( AIPMT 2004)
Two springs of spring constants k1 and k2 are joined in series. The effective spring constant of the combination is given by
A.
B. (k1 + k2)/2
C. k1 + k2
D. k1k2/(k1 + k2)
7. ⇒ (AIPMT 2003)
The time period of mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
A. T/4
B. T
C. T/2
D. 2T
8. ⇒ (AIPMT 2002)
A mass is suspended separately by two different springs in (successive order then time periods is
t1 and t2 respectively, If it is connected by both spring as shown in figure then
time period is t0 , the correct relation is
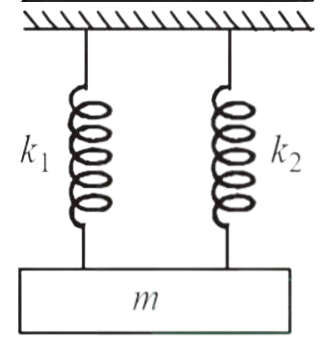
A.
B.
C.
D.
Correct Answer is Option (B)
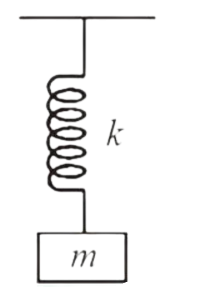
The time period of a spring mass system as shown in figure 1 is given by , where k is the spring constant.
...(i)
and ...(ii)
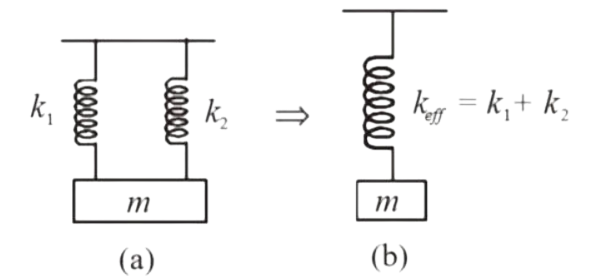
Now, when they are connected in parallel as shown in figure 2(a), the system can be replaced
by a single spring of spring constant, keff = k1 + k2.
[Since mg = k1x + k2x = keffx]
...(iii)
From (i), ...(iv)
From (ii), ...(v)
From (ii), ...(vi)
Now (iv) + (v)