JEE Main SHM PYQ

21.(JEE Main 2020 (Online) 9th January Evening Slot)

A spring mass system (mass m, spring constant k and natural length $l$ ) rest in equilibrium on a horizontal disc. The free end of the spring is fixed at the centre of the disc. If the disc together with spring mass system, rotates about it's axis with an angular velocity $ω$ , (k $≫ m ω^{2}$ ) the relative change in the length of the spring is best given by the option :

A. $\frac{m ω^{2}}{3 k}$

B. $\frac{m ω^{2}}{k}$

C. $\frac{2 m ω^{2}}{k}$

D. $\sqrt{\frac{2}{3}} (\frac{m ω^{2}}{k})$

Correct Answer is Option (B)

m $ω^{2}$ (l₀ + x) = kx

x = $\frac{m I_{0} ω^{2}}{k - m ω^{2}}$

For k >> m $ω^{2}$

$\frac{x}{I_{0}} = \frac{m ω^{2}}{k}$

22.(JEE Main 2017 (Online) 8th April Morning Slot)

A 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is :

A. $\frac{1}{4} H z$

B. $\frac{1}{2 \sqrt{2}} H z$

C. $\frac{1}{2} H z$

D. 2 Hz

Correct Answer is Option (C)

For 1 kg block :

JEE Main 2017 (Online) 8th April Morning Slot Physics - Simple Harmonic Motion Question 101 English Explanation 1

Here frequency of spring (f) = $\frac{1}{2 π} \sqrt{\frac{k}{m}}$

Given that, F = 1 Hz

$∴$ $\frac{1}{2 π} \sqrt{\frac{k}{1}}$ = 1

$\Rightarrow$ k = 4 $π$ ² N m^{$-$ 1}

For 8 kg Block :

JEE Main 2017 (Online) 8th April Morning Slot Physics - Simple Harmonic Motion Question 101 English Explanation 2

Here two identical springs are attached in parallel. So,

K_eq = k + k = 2k

$∴$ Frequency of 8 kg block,

F' = $\frac{1}{2 π} \sqrt{\frac{k_{e q}}{m^{'}}}$

= $\frac{1}{2 π} \sqrt{\frac{2 k}{8}}$

= $\frac{1}{2 π} \sqrt{\frac{2 \times 4 π^{2}}{8}}$

= $\frac{1}{2 π} \times π$

= $\frac{1}{2}$ Hz

23.(AIEEE 2007)

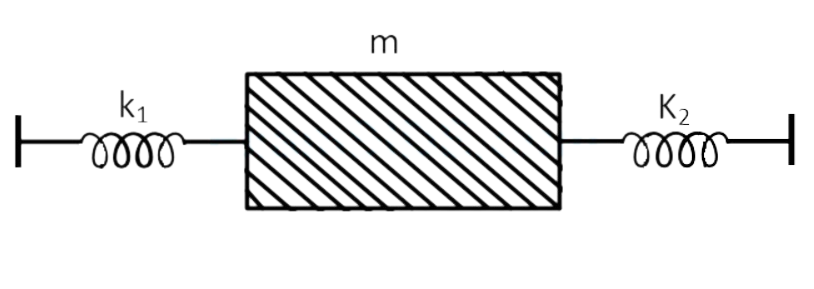
Two springs, of force constant $k_{1}$ and $k_{2}$ are connected to a mass $m$ as shown. The frequency of oscillation of the mass is $f .$ If both $k_{1}$ and $k_{2}$ are made four times their original values, the frequency of oscillation becomes AIEEE 2007 Physics - Simple Harmonic Motion Question 120 English

A. 2f

B. f/2

C. f/4

D. 4f

Correct Answer is Option (A)

The two springs are in parallel.

$f = \frac{1}{2 π} \sqrt{\frac{K_{1} + K_{2}}{m}} . . . (i)$

$f^{'} = \frac{1}{2 π} \sqrt{\frac{4 K_{1} + 4 K_{2}}{m}}$

$= \frac{1}{2 π} \sqrt{\frac{4 (K_{1} + 4 K_{2})}{m}}$

$= 2 (\frac{1}{2 π} \sqrt{\frac{K_{1} + K_{2}}{m}})$

$= 2 f$ from eqn. $(i)$

24.(AIEEE 2004)

A particle at the end of a spring executes $S . H . M$ with a period $t_{1}$ . While the corresponding period for another spring is $t_{2}$ . If the period of oscillation with the two springs in series is $T$ then

A. $T^{- 1} = t_{1}^{- 1} + t_{2}^{- 1}$

C. $T = t_{1} + t_{2}$

D. $T^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$

Correct Answer is Option (B)

For first spring, $t_{1} = 2 π \sqrt{\frac{m}{k_{1}}},$

For second spring, $t_{2} = 2 π \sqrt{\frac{m}{k_{2}}}$

when springs are in series then, $k_{e f f} = \frac{k_{1} k_{2}}{k_{1} + k_{2}}$

$∴$ $T = 2 π \sqrt{\frac{m (k_{1} + k_{2})}{k_{1} k_{2}}}$

$∴$ $T = 2 π \sqrt{\frac{m}{k_{2}} + \frac{m}{k_{1}}}$

$= 2 π \sqrt{\frac{t_{2}^{2}}{{(2 π)}^{2}} + \frac{t_{1}^{2}}{{(2 π)}^{2}}}$

$\Rightarrow T^{2} = t_{1}^{2} + t_{2}^{2}$

25.(AIEEE 2003)

A mass $M$ is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes $S H M$ of time period $T .$ If the mass is increased by $m .$ the time period becomes $\frac{5 T}{3}$ . Then the ratio of $\frac{m}{M}$ is :

A. $\frac{3}{5}$

B. $\frac{25}{9}$

C. $\frac{16}{9}$

D. $\frac{5}{3}$

Correct Answer is Option (C)

The time period of a simple harmonic motion (SHM) performed by a mass-spring system is given by the formula:

$T = 2 π \sqrt{\frac{M}{k}}$

where:

T is the time period,
M is the mass of the object, and
k is the spring constant.

We know that if the mass is increased by m, the time period becomes $\frac{5 T}{3}$ . We can set up an equation for this new scenario:

$\frac{5 T}{3} = 2 π \sqrt{\frac{M + m}{k}}$

Since we know that $T = 2 π \sqrt{\frac{M}{k}}$ , we can substitute T in the equation above:

$\frac{5}{3} \cdot 2 π \sqrt{\frac{M}{k}} = 2 π \sqrt{\frac{M + m}{k}}$

Squaring both sides of the equation to eliminate the square root, we get:

$\frac{25}{9} \cdot \frac{M}{k} = \frac{M + m}{k}$

Solving for $\frac{m}{M}$ , we get:

$\frac{m}{M} = \frac{25}{9} - 1 = \frac{16}{9}$