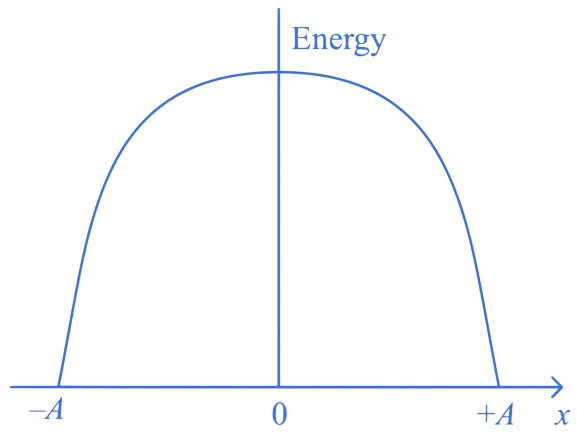
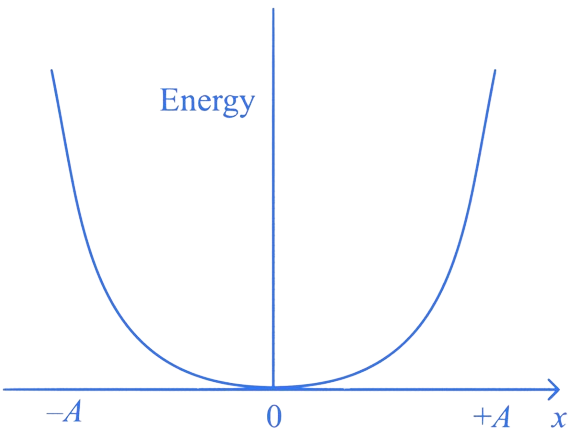
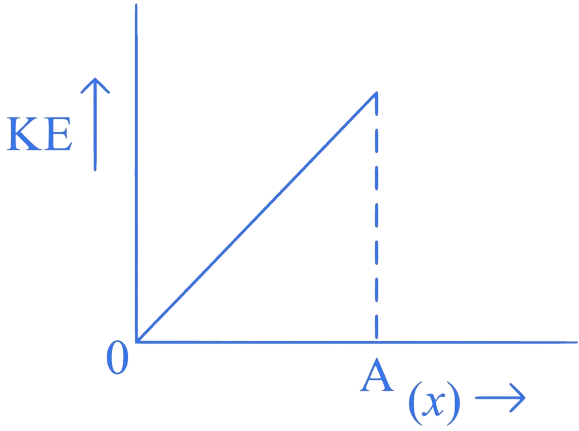
Correct Answer is Option (A)

The total energy of a particle executing simple harmonic motion (SHM) is given by:

$E=\frac{1}{2}m{\omega }^2{A}^2$

where $m$ is the mass of the particle, $\omega$ is the angular frequency of the SHM, and $A$ is the amplitude of the motion.

At any point during SHM, the kinetic energy of the particle is given by:

$K=\frac{1}{2}m{\omega }^2(x^2+A^2{\cos }^2\omega t)$

where $x$ is the displacement of the particle from the mean position.

The potential energy of the particle at the same point is given by:

$U=\frac{1}{2}m{\omega }^2(x^2+A^2{\sin }^2\omega t)$

When the kinetic energy becomes equal to the potential energy, we have:

$K=U$

$\frac{1}{2}m{\omega }^2(x^2+A^2{\cos }^2\omega t)=\frac{1}{2}m{\omega }^2(x^2+A^2{\sin }^2\omega t)$

Simplifying this equation, we get:

$x^2=\frac{1}{2}{A}^2$

$x=\pm \frac{1}{\sqrt{2}}A$

Therefore, the distance from the mean position when the kinetic energy becomes equal to the potential energy is $\boxed{{\displaystyle \frac{1}{\sqrt{2}}A}}$

Correct Answer is Option (A)

$\begin{array}{rl}& \text{T.E. }-\text{ P.E. }=\text{ K.E. }\\ \\ & \text{K.E. }=\frac{1}{2}m{\omega }^2(A^2-x^2)\end{array}$

Which is the equation of downward parabola.

Correct Answer is Option (D)

Let's denote the amplitude of the simple harmonic motion as A, and the displacement of the particle from the mean position as x. The given condition is that x = A/2.

For a particle in SHM, the potential energy (PE) is given by:

$PE=\frac{1}{2}k{x}^2$

And the total mechanical energy (E) of the particle remains constant and is given by:

$E=\frac{1}{2}k{A}^2$

Since the total mechanical energy is the sum of potential energy and kinetic energy (KE), we have:

$E=PE+KE$

Now, we need to find the ratio of potential energy to kinetic energy when x = A/2.

Calculate the potential energy at x = A/2:

$PE=\frac{1}{2}k{\left(\frac{A}{2}\right)}^2=\frac{1}{8}k{A}^2$

Substitute the expression for total mechanical energy:

$KE=E-PE=\frac{1}{2}k{A}^2-\frac{1}{8}k{A}^2=\frac{3}{8}k{A}^2$

Now, find the ratio of potential energy to kinetic energy:

$\frac{PE}{KE}=\frac{\frac{1}{8}k{A}^2}{\frac{3}{8}k{A}^2}=\frac{1}{3}$

Therefore, the ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude is 1 : 3.

Correct Answer is Option (C)

For a particle executing SHM

$\mathrm{KE}=\frac{1}{2}\mathrm{m}{\omega }^2({\mathrm{A}}^2-{\mathrm{x}}^2)$

When $\mathrm{x}=0,$ KE is maximum & when $\mathrm{x}=\mathrm{A},$ KE is zero and KE vs x graph is parabola.

Correct Answer is Option (C)

${\mathrm{U}}_{max}=\frac{1}{2}\mathrm{m}{\omega }^2{\mathrm{A}}^2=25\mathrm{J}$

$\mathrm{KE}$ at $\frac{\mathrm{A}}{2}=\frac{1}{2}m{v}_1^2=\frac{1}{2}m{\omega }^2(A^2-\frac{A^2}{4})$

$=\frac{1}{2}\mathrm{m}{\omega }^2\frac{3{\mathrm{A}}^2}{4}=\frac{3}{4}\left(\frac{1}{2}\mathrm{m}{\omega }^2{\mathrm{A}}^2\right)$

$\mathrm{KE}=\frac{3}{4}\times 25=18.75\mathrm{J}$