JEE Main Work, Energy and Power PYQ

1.(JEE Main 2024 (Online) 5th April Morning Shift )

A body of mass $50 kg$ is lifted to a height of $20 m$ from the ground in the two different ways as shown in the figures. The ratio of work done against the gravity in both the respective cases, will be :

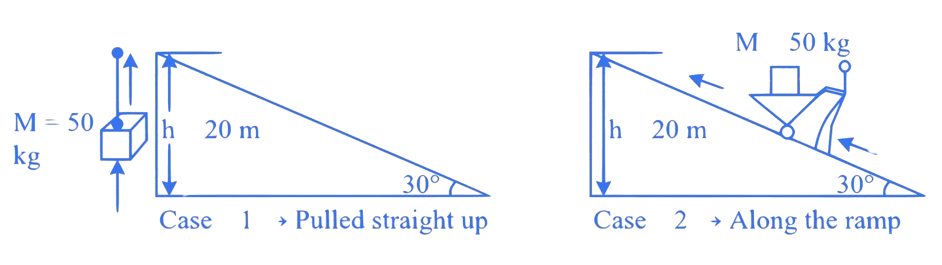
JEE Main 2024 (Online) 5th April Morning Shift Physics - Work Power & Energy Question 5 English

A. $2 : 1$

B. $\sqrt{3} : 2$

C. $1 : 1$

D. $1 : 2$

Correct option is (C)

Work done in both cases is equal to $- m g Δ h$

$∴ Ratio = 1 : 1$

2.(JEE Main 2024 (Online) 30th January Evening Shift )

A block of mass $1 kg$ is pushed up a surface inclined to horizontal at an angle of $60^{\circ}$ by a force of $10 N$ parallel to the inclined surface as shown in figure. When the block is pushed up by $10 m$ along inclined surface, the work done against frictional force is :

$[g = 10 m / s^{2}]$

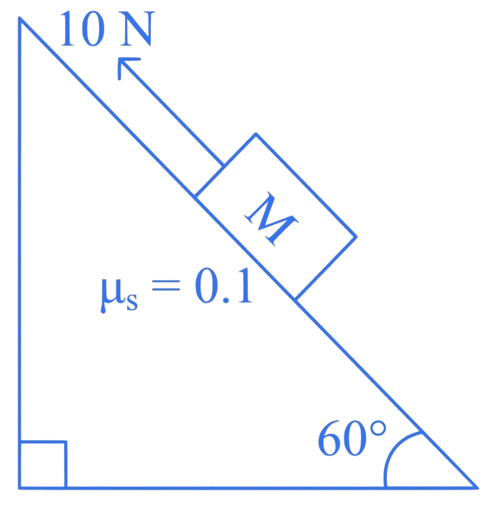
JEE Main 2024 (Online) 30th January Evening Shift Physics - Work Power & Energy Question 12 English

A.5 $\sqrt{3}$ J

B.5 J

C. $5 \times 10^{3}$ J

D.10 J

Correct option is (B)

Work done again frictional force

$\begin{aligned} = μ N \times 10 \\ = 0.1 \times 5 \times 10 = 5 J \end{aligned}$

3.(JEE Main 2024 (Online) 9th April Evening Shift )

A force $(3 x^{2} + 2 x - 5) N$ displaces a body from $x = 2 m$ to $x = 4 m$ . Work done by this force is ________ J.

Correct answer is 58

To find the work done by the force when the body is displaced from $x = 2 m$ to $x = 4 m$ , we use the formula for work done by a variable force in one dimension, which is the integral of the force with respect to displacement:

$W = \int_{x_{1}}^{x_{2}} F d x$

Given the force $F (x) = (3 x^{2} + 2 x - 5) N$ and the limits of integration from $x = 2 m$ to $x = 4 m$ , we can substitute these values into the equation:

$W = \int_{2}^{4} (3 x^{2} + 2 x - 5) d x$

Calculating the integral, we get:

$W = {[\frac{3 x^{3}}{3} + \frac{2 x^{2}}{2} - 5 x]}_{2}^{4}$

This simplifies to:

$W = {[x^{3} + x^{2} - 5 x]}_{2}^{4}$

Substituting the upper limit ( $x = 4$ ) and then the lower limit ( $x = 2$ ) into the antiderivative, and subtracting the latter from the former, we get:

$W = [(4)^{3} + (4)^{2} - 5 (4)] - [(2)^{3} + (2)^{2} - 5 (2)]$

$W = (64 + 16 - 20) - (8 + 4 - 10)$

$W = 60 - 2$

$W = 58 J$

Therefore, the work done by the force as the body displaces from $x = 2 m$ to $x = 4 m$ is $58 J$ .

4(JEE Main 2023 (Online) 29th January Evening Shift )

Identify the correct statements from the following :

A. Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket is negative.

B. Work done by gravitational force in lifting a bucket out of a well by a rope tied to the bucket is negative.

C. Work done by friction on a body sliding down an inclined plane is positive.

D. Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity is zero.

E. Work done by the air resistance on an oscillating pendulum is negative.

Choose the correct answer from the options given below :

A. A and C only

B. B and D only

C. B, D and E only

D. B and E only

Correct Option is (D)

When a man lifts a bucket out of a well using a rope, work is done by the man and the gravitational force. The work done by the man is positive as he has to exert an upward force to lift the bucket. The work done by the gravitational force is negative because the direction of the force is opposite to the direction of displacement.

Therefore, the statement (A) "Work done by a man in lifting a bucket out of a well by means of rope tied to the bucket is negative." is incorrect.

Therefore, the statement (B) "Work done by gravitational force in lifting a bucket out of a well by a rope tied to the bucket is negative." is correct.

Work is defined as the product of force and displacement in the direction of the force. When a body slides down an inclined plane, the force of friction acts against the motion of the body, opposing its descent.

The direction of the force of friction is opposite to the direction of the displacement of the body, which is downwards. Hence, the work done by the force of friction is negative.

Therefore, the statement (C) "Work done by friction on a body sliding down an inclined plane is positive" is incorrect.

If the body is moving on a rough horizontal plane, there will be friction present, which will act in the opposite direction to the applied force. The force of friction will oppose the motion of the body, reducing its velocity. As a result, the net work done on the body will not be zero, as the force of friction and the applied force will not cancel each other out completely.

Therefore, the statement (D) "Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity is zero." is incorrect.

Statement E: "Work done by the air resistance on an oscillating pendulum is negative."

This statement refers to the work done by the air resistance on an oscillating pendulum, which is a physical system that swings back and forth under the influence of gravity.

As the pendulum oscillates, it experiences air resistance, which opposes its motion and slows it down. The direction of the air resistance force is opposite to the direction of the displacement of the pendulum, which is back and forth.

Hence, the work done by the air resistance force is negative, as the direction of the force and the displacement are opposite.

Therefore, the statement (E) "Work done by the air resistance on an oscillating pendulum is negative" is correct.

5.(JEE Main 2023 (Online) 15th April Morning Shift )

A block of mass $10 kg$ is moving along $x$ -axis under the action of force $F = 5 x N$ . The work done by the force in moving the block from $x = 2 m$ to $4 m$ will be __________ J.

Correct answer is (30)

To calculate the work done by the force $F = 5 x$ in moving the block from $x = 2 m$ to $x = 4 m$ , we can use the formula for work done by a variable force:

$W = \int_{x_{1}}^{x_{2}} F (x) d x$

In this case, $F (x) = 5 x$ , $x_{1} = 2 m$ , and $x_{2} = 4 m$ . Now, we can substitute these values into the formula and evaluate the integral:

$W = \int_{2}^{4} 5 x d x$

To evaluate the integral, we find the antiderivative of $5 x$ :

$\int 5 x d x = \frac{5}{2} x^{2} + C$

Now, we can find the work done by evaluating the antiderivative at the limits of integration:

$W = {[\frac{5}{2} x^{2}]}_{2}^{4} = \frac{5}{2} (4^{2}) - \frac{5}{2} (2^{2})$

$W = \frac{5}{2} (16) - \frac{5}{2} (4) = 40 - 10 = 30 J$

The work done by the force in moving the block from $x = 2 m$ to $x = 4 m$ is 30 J.