JEE Main Motion in Straight Line PYQ

21. (AIEEE 2005 )

A car starting from rest accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate $\frac{f}{2}$ to come to rest. If the total distance traversed is 15 S, then

A. $S = \frac{1}{6} f t^{2}$

B. $S = f t$

C. $S = \frac{1}{4} f t^{2}$

D. $S = \frac{1}{72} f t^{2}$

Correct Option is (D)

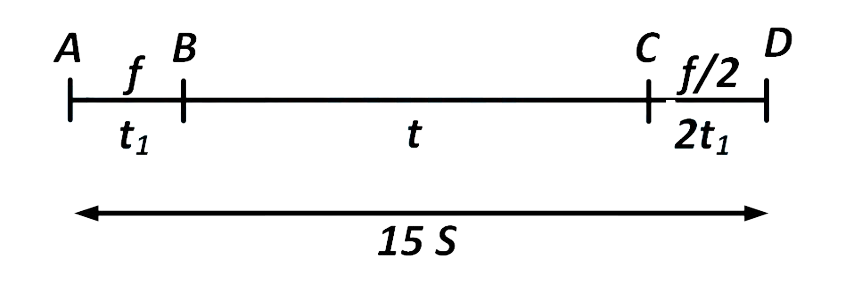AIEEE 2005 Physics - Motion Question 153 English Explanation Initially car starts from rest so u = 0.

Now distance from $A$ to $B$ ,

$S = \frac{1}{2} f t_{1}^{2}$

$\Rightarrow f t_{1}^{2} = 2 S$

Distance from $B$ to $C$ $= (f t_{1}) t$

In B to C velocity is constant and v = $f t_{1}$

Distance from $C$ to $D$
$= \frac{u^{2}}{2 a} = \frac{{(f t_{1})}^{2}}{2 (f / 2)} = f t_{1}^{2} = 2 S$

$\Rightarrow S + f t_{1} t + 2 S = 15 S$

$\Rightarrow f t_{1} t = 12 S$ ........(1)

But $\frac{1}{2} f t_{1}^{2} = S$ .........(2)

On dividing the above two equations, we get $t_{1} = \frac{t}{6}$

$\Rightarrow S = \frac{1}{2} f {(\frac{t}{6})}^{2} = \frac{f t^{2}}{72}$

22. (AIEEE 2004 )

An automobile travelling with speed of 60 km/h, can brake to stop within a distance of 20 m. If the car is going twice as fast, i.e 120 km/h, the stopping distance will be

A. 60 m

B. 40 m

C. 20 m

D. 80 m

Correct Option is (A)

Assume $a$ be the retardation for both the vehicle then

In case of automobile,

$u_{1}^{2} - 2 a s_{1} = 0$

$\Rightarrow u_{1}^{2} = 2 a s_{1}$

And in case for car,

$u_{2}^{2} = 2 a s_{2}$

$∴$ ${(\frac{u_{2}}{u_{1}})}^{2} = \frac{s_{2}}{s_{1}}$

$\Rightarrow {(\frac{120}{60})}^{2} = \frac{s_{2}}{20}$

$\Rightarrow$ s₂ = 80 m

23. (AIEEE 2003 )

A car, moving with a speed of 50 km/hr, can be stopped by brakes after at least 6 m. If the same car is moving at a speed of 100 km/hr, the minimum stopping distance is

A. 12 m

B. 18 m

C. 24 m

D. 6 m

Correct Option is (C)

For case 1 :
u = 50 km/hr = $\frac{50 \times 1000}{3600}$ m/s = $\frac{125}{9}$ m/s, v = 0, s = 6 m, $a$ = ?

$∴$ 0² = u² + 2 $a$ s

$\Rightarrow$ $a = - \frac{u^{2}}{2 s}$

$\Rightarrow$ $a = - \frac{{(\frac{125}{9})}^{2}}{2 \times 6}$ = $-$ 16 m/s²

For case 2 :
u = 100 km/hr = $\frac{100 \times 1000}{3600}$ m/s = $\frac{250}{9}$ m/s, v = 0, $a$ = $-$ 16, s = ?

$∴$ 0² = u² + 2 $a$ s

$\Rightarrow$ $s = - \frac{u^{2}}{2 a}$

$\Rightarrow$ $s = - \frac{{(\frac{250}{9})}^{2}}{2 \times - 16}$ = 24 m