Correct option is (b)
1. . (JEE Main 2024 (Online) 6th April Evening Shift )
A body projected vertically upwards with a certain speed from the top of a tower reaches the ground in . If it is projected vertically downwards from the same point with the same speed, it reaches the ground in . Time required to reach the ground, if it is dropped from the top of the tower, is :
A.
B.
C.
D. /p>
Correct option is (b)
2. . (JEE Main 2024 (Online) 27th January Evening Shift )
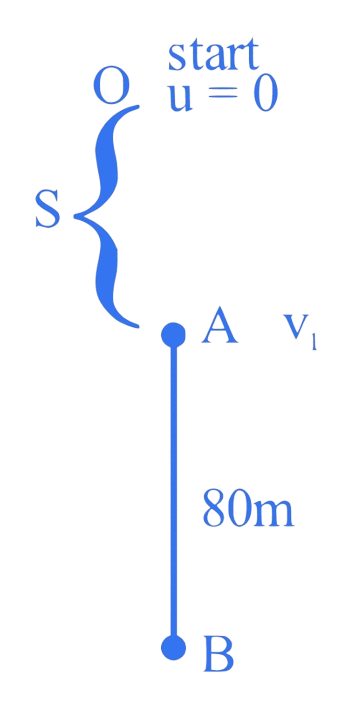
A body falling under gravity covers two points and separated by in . The distance of upper point A from the starting point is _________ (use ).
Correct answer is 45
To find the distance of the upper point A from the starting point, we need to first understand the motion of a freely falling body under the influence of gravity. The body falling under gravity is an example of uniformly accelerated motion with the acceleration equal to the acceleration due to gravity, which is given as .
We will consider point A where the body was at time and point B where the body was at time . The displacement in these 2 seconds is given to be 80 meters.
For an object under constant acceleration, the displacement can be found using the equation:
where
is the initial velocity,
is the time,
is the acceleration,
is the displacement.
Since the body falls under gravity, its initial velocity at the starting point is 0 (), thus the equation simplifies to:
Let's denote the distance of point A from the starting point as and the distance of point B as . We know the body covers meters in seconds from A to B, so we can write:
We can calculate the distance covered till point B (in time ) as:
And the distance covered till point A (in time ) as:
Now, substituting and in our difference equation:
Therefore, time at point A is seconds. To find , we can use the above simplified motion equation:
So, the distance of the upper point A from the starting point is .
Alternate Method :
3. (JEE Main 2023 (Online) 12th April Morning Shift)
A ball is thrown vertically upward with an initial velocity of . The ratio of velocity after and is . The value of is ___________.
take,
A.
B. 10
C. 5
D. 6
Correct Option is (C)
To solve this problem, we can use the following equation of motion for the vertical velocity at
any given time
:
Where:
-
is the final velocity at time
-
is the initial velocity (150 m/s)
-
is the acceleration due to gravity (10 m/s²)
-
is the time in seconds
First, we need to find the velocities at
and
.
For
:
For
:
Now we need to find the ratio of these velocities:
Next, we can set up an equation to find the value of
:
Now, we can solve for
:
The value of
is 5.
4. (JEE Main 2023 (Online) 31st January Morning Shift )
Spherical insulating ball and a spherical metallic ball of same size and mass are dropped from the same height. Choose the correct statement out of the following {Assume negligible air friction}
A. Metal ball will reach the earth's surface earlier than the insulating ball
B. Both will reach the earth's surface simultaneously.
C. Insulating ball will reach the earth's surface earlier than the metal ball
D. Time taken by them to reach the earth's surface will be independent of the properties of their materials
Correct Option is (C)
The correct answer is option C: the insulating ball will reach the earth's surface earlier than
the metal ball.
When the two balls are dropped from the same height, they will experience the same
gravitational force, which will cause them to accelerate downwards. However, According to
Faraday’s law of electromagnetic induction motion of metal is opposed by earth magnetic field.
Which will slightly reduce its acceleration.
On the other hand, the insulating ball will not experience any electromagnetic
induction. Therefore, it will accelerate downwards at a slightly faster rate than the metal
ball. As a result, the insulating ball will reach the earth's surface earlier than the metal
ball.
So, option C is the correct statement.
5. (JEE Main 2022 (Online) 29th July Evening Shift )
A juggler throws balls vertically upwards with same initial velocity in air. When the first ball reaches its highest position, he throws the next ball. Assuming the juggler throws n balls per second, the maximum height the balls can reach is
A. g/2n
B. g/n
C. 2gn
D. g/2n2
Correct Option is (D)
The juggler throws n balls per second.
Interval between balls = seconds
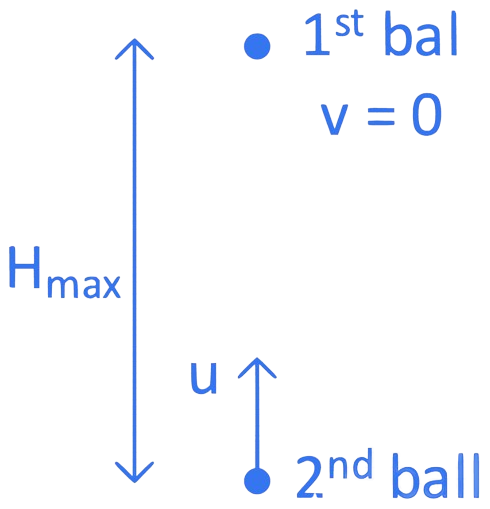
At maximum height velocity of first ball
Juggler throws all balls with same initial velocity
For 1st ball,
, , ,
Using formula,
...... (1)
And using formula,
Time taken by ball 1 to reach maximum height
According to the question,
....... (2)
Putting value of in equation (1), we get