Correct answer option is (C)
For hollow sphere
For solid cylinder
1. (JEE Main 2024 (Online) 5th April Morning Shift )
Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of Inertia about their diameter axis as shown in figure is . The value of is :
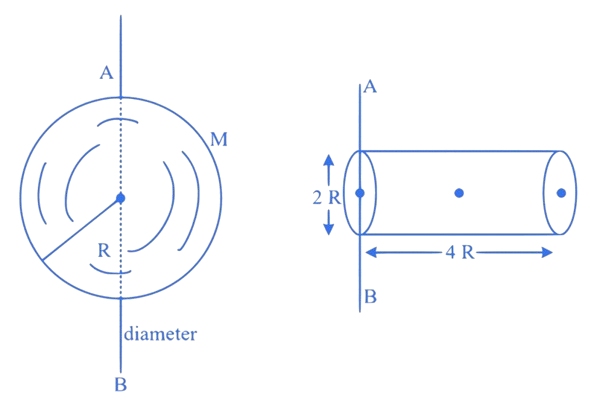
A. 34
B. 51
C. 67
D. 17
Correct answer option is (C)
For hollow sphere
For solid cylinder
2. (JEE Main 2024 (Online) 6th April Evening Shift )
Three balls of masses and respectively are arranged at centre of the edges of an equilateral triangle of side . The moment of inertia of the system about an axis through the centroid and perpendicular to the plane of triangle, will be ________ .
Correct answer is 4
Distance between centroid and midpoint of sides
3. (JEE Main 2024 (Online) 5th April Evening Shift )
A hollow sphere is rolling on a plane surface about its axis of symmetry. The ratio of rotational kinetic energy to its total kinetic energy is . The value of is _________.
Correct answer is 2
For a hollow sphere rolling on a plane surface without slipping, its total kinetic energy (K.E.) is the sum of its translational kinetic energy and rotational kinetic energy. The translational kinetic energy results from the motion of the center of mass of the sphere, and the rotational kinetic energy is due to its rotation about an axis through its center of mass (in this case, the axis of symmetry).
The translational kinetic energy (TKE) can be expressed as:
Where:
The rotational kinetic energy (RKE) for a rolling object can be given by:
For a hollow sphere, the moment of inertia (I) about its axis of symmetry is:
where r is the radius of the sphere. The angular velocity, , can be related to the linear velocity, v, by the relation , for an object rolling without slipping. We substitute into the expression for RKE:
This simplifies to:
The total kinetic energy (Total K.E.) of the rolling hollow sphere is the sum of its translational and rotational kinetic energies:
Now, we want to find the ratio of the rotational kinetic energy to the total kinetic energy:
Since the mass and velocity are common in both the numerator and the denominator, they will cancel out, leaving:
Therefore, the value of , representing the ratio of the rotational kinetic energy to the total kinetic energy for a hollow sphere rolling on a plane surface about its axis of symmetry, is . Thus, .
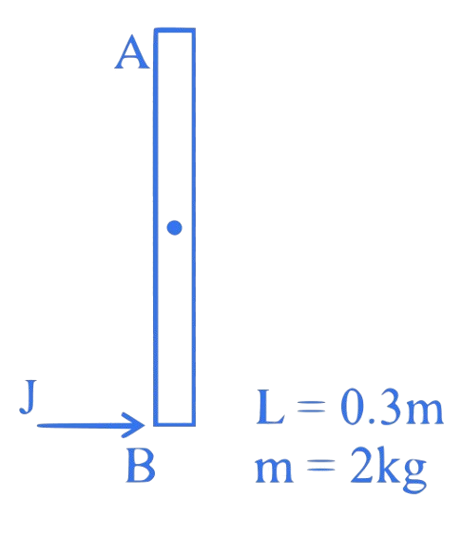
4. (JEE Main 2024 (Online) 1st February Evening Shift )
A uniform rod of mass and length at rest on a smooth horizontal surface. An impulse of force is applied to end B. The time taken by the rod to turn through at right angles will be , where _______ .
Correct answer is 4
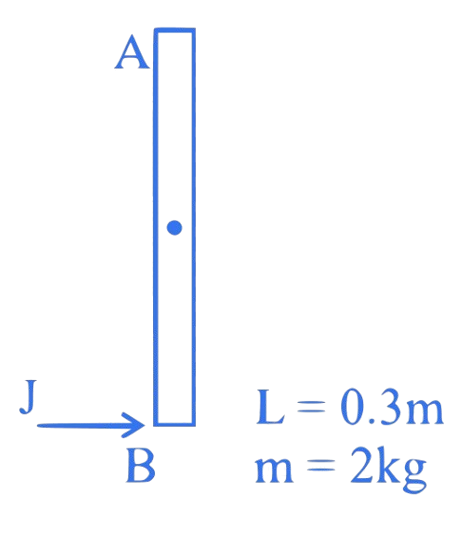
Impulse
Angular impuls
5. (JEE Main 2024 (Online) 31st January Evening Shift )
Two identical spheres each of mass and radius are fixed at the ends of a light rod so that the separation between the centers is . Then, moment of inertia of the system about an axis perpendicular to the rod and passing through its middle point is , where the value of is ___________.
Correct answer is 53