JEE Main Rotational Motion PYQ

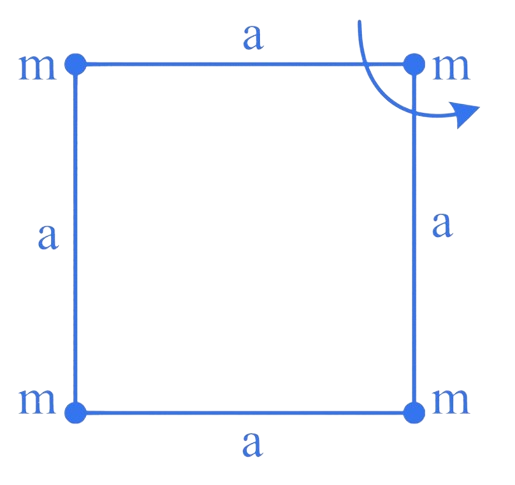
6. (JEE Main 2024 (Online) 27th January Morning Shift )

Four particles each of mass $1 kg$ are placed at four corners of a square of side $2 m$ . Moment of inertia of system about an axis perpendicular to its plane and passing through one of its vertex is _____ ${kgm}^{2}$ .

JEE Main 2024 (Online) 27th January Morning Shift Physics - Rotational Motion Question 18 English

Correct answer is 16

JEE Main 2024 (Online) 27th January Morning Shift Physics - Rotational Motion Question 18 English Explanation

$\begin{aligned} I = {ma}^{2} + {ma}^{2} + m (\sqrt{2 a})^{2} \\ = 4 {ma}^{2} \\ = 4 \times 1 \times (2)^{2} = 16 \end{aligned}$

7. (JEE Main 2023 (Online) 10th April Evening Shift)

Given below are two statements: one is labelled as Assertion $A$ and the other is labelled as Reason $R$

Assertion A : An electric fan continues to rotate for some time after the current is switched off.

Reason R : Fan continues to rotate due to inertia of motion.

In the light of above statements, choose the most appropriate answer from the options given below.

A. A is not correct but R is correct

B. A is correct but R is not correct

C. Both A and R are correct and R is the correct explanation of A

D. Both A and R are correct but R is NOT the correct explanation of A

Correct Answer is Option (C)

The correct answer is Both A and R are correct and R is the correct explanation of A.

Explanation:

Assertion A: An electric fan continues to rotate for some time after the current is switched off. This is a correct statement. When you switch off the fan, it doesn't stop immediately but continues to rotate for some time.

Reason R: Fan continues to rotate due to inertia of motion. This is also a correct statement. Inertia is the resistance of any physical object to any change in its state of motion. This includes changes to the object's speed or direction of motion. An object will stay in its state of motion unless a force acts on it. In the case of the fan, after the current is switched off, the fan blades have inertia and continue to move due to this inertia until the frictional forces (like air resistance and friction in the fan's bearings) cause it to stop. Therefore, inertia of motion is the correct reason for the fan's continued motion after the current is switched off.

8. (JEE Main 2023 (Online) 15th April Morning Shift )

A solid sphere and a solid cylinder of same mass and radius are rolling on a horizontal surface without slipping. The ratio of their radius of gyrations respectively $(k_{sph} : k_{cyl})$ is $2 : \sqrt{x}$ . The value of $x$ is ____________ .

Correct answer is (5)

Let the mass of both the solid sphere and the solid cylinder be $M$ , and let their common radius be $R$ . The moment of inertia $I$ of a solid sphere and a solid cylinder are given by:

$I_{s p h} = \frac{2}{5} M R^{2}$

$I_{c y l} = \frac{1}{2} M R^{2}$

The radius of gyration $k$ is related to the moment of inertia $I$ by the formula $I = M k^{2}$ . Therefore, we can find the radius of gyration for both the solid sphere and the solid cylinder using their respective moments of inertia:

$k_{s p h}^{2} = \frac{I_{s p h}}{M} = \frac{2}{5} R^{2}$

$k_{c y l}^{2} = \frac{I_{c y l}}{M} = \frac{1}{2} R^{2}$

Now, let's find the ratio of their radius of gyrations:

$\frac{k_{s p h}}{k_{c y l}} = \frac{2}{\sqrt{x}}$

Squaring both sides:

$\frac{k_{s p h}^{2}}{k_{c y l}^{2}} = \frac{4}{x}$

Substituting the expressions for $k_{s p h}^{2}$ and $k_{c y l}^{2}$ :

$\frac{\frac{2}{5} R^{2}}{\frac{1}{2} R^{2}} = \frac{4}{x}$

Simplifying and solving for $x$ :

$\frac{2}{5} \cdot \frac{2}{1} = \frac{4}{x}$

$\frac{4}{5} = \frac{4}{x}$

Thus, $x = 5$ .

9. (JEE Main 2023 (Online) 8th April Morning Shift )

The moment of inertia of a semicircular ring about an axis, passing through the center and perpendicular to the plane of ring, is $\frac{1}{x} {MR}^{2}$ , where $R$ is the radius and $M$ is the mass of the semicircular ring. The value of $x$ will be __________.

Correct answer is (1)

The moment of inertia of semicircular ring about axis passing through centre of ring and perpendicular to plane of ring is $= {MR}^{2}$ , so $x = 1$ .

10. (JEE Main 2023 (Online) 6th April Evening Shift )

A ring and a solid sphere rotating about an axis passing through their centers have same radii of gyration. The axis of rotation is perpendicular to plane of ring. The ratio of radius of ring to that of sphere is $\sqrt{\frac{2}{x}}$ . The value of $x$ is ___________.

Correct answer is (5)

Given that the radii of gyration for the ring and the solid sphere are equal, we have:

$K_{1} = K_{2}$

For the ring, the moment of inertia is:

$I_{r i n g} = m R_{1}^{2} = m K_{1}^{2}$

Thus, the radius of gyration for the ring is:

$K_{1} = R_{1}$

For the solid sphere, the moment of inertia is:

$I_{s p h e r e} = \frac{2}{5} m^{'} R_{2}^{2} = m^{'} K_{2}^{2}$

Hence, the radius of gyration for the solid sphere is:

$K_{2} = \sqrt{\frac{2}{5}} R_{2}$

Since the radii of gyration are equal:

$R_{1} = \sqrt{\frac{2}{5}} R_{2}$

Therefore, the ratio of the radius of the ring to that of the sphere is:

$\frac{R_{1}}{R_{2}} = \sqrt{\frac{2}{5}}$

So, the value of $x$ is:

$x = 5$