Correct Answer is Option (A)
We know Rotational Kinetic Energy
Angular Momentum
Initial
Final = =
41. (AIEEE 2003)
A particle performing uniform circular motion has angular frequency is doubled & its kinetic energy halved, then the new angular momentum is
A.
B. 2L
C. 4L
D.
Correct Answer is Option (A)
We know Rotational Kinetic Energy
Angular Momentum
Initial
Final = =
42. (AIEEE 2002)
Initial angular velocity of a circular disc of mass is Then two small spheres of mass are attached gently to diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc?
A.
B.
C.
D.
Correct Answer is Option (C)
When two small spheres of mass are attached gently, the external
torque, about the axis of rotation, is zero.
So, = 0
= conserved
So the angular momentum about the axis of rotation is conserved.
Here Moment of inertia of Disc and
After adding two sphere Moment of Inertia of disc and two sphere,
43. (AIEEE 2002)
A particle of mass moves along line PC with velocity as shown. What is the angular momentum of the
particle about P?
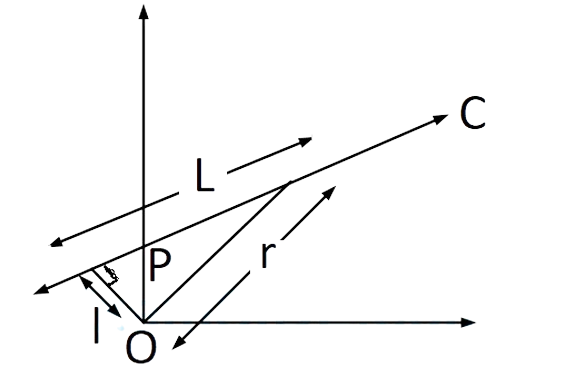
A. mvL
B. mvl
C. mvr
D. zero
Correct Answer is Option (D)
Angular momentum
( linear momentum ) ( perpendicular distance of the line of
action of momentum from the axis of rotation)
[ Here because the particle is
moving through the line PQ and
r is the perpendicular distance from line PQ of the particle ]