Correct Answer is Option (C)
6. (JEE Main 2023 (Online) 13th April Morning Shift)
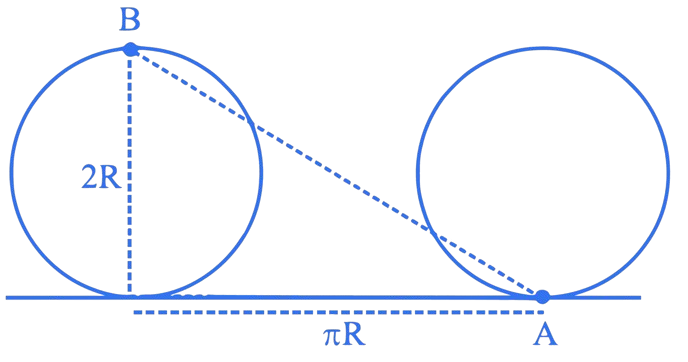
A disc is rolling without slipping on a surface. The radius of the disc is . At , the top most point on the disc is as shown in figure. When the disc completes half of its rotation, the displacement of point A from its initial position is
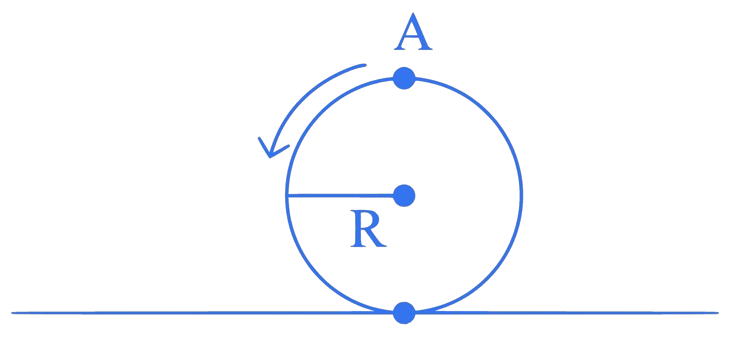
A.
B. 2R
C.
D.
Correct Answer is Option (C)

7. (JEE Main 2023 (Online) 13th April Morning Shift )
A solid sphere is rolling on a horizontal plane without slipping. If the ratio of angular momentum about axis of rotation of the sphere to the total energy of moving sphere is then, the value of its angular speed will be ____________ .
Correct answer is (4)
Given that the solid sphere is rolling without slipping, we
have:
Angular momentum
Kinetic energy
For a solid sphere, the moment of inertia is , and the relationship between linear and
angular velocity is .
Substituting these values into the expressions for and :
Now, the given ratio of is :
Since , we can substitute this relationship into
the equation and solve for :
Thus, the value of the angular speed is .
8. (JEE Main 2023 (Online) 12th April Morning Shift )
For a rolling spherical shell, the ratio of rotational kinetic energy and total kinetic energy is . The value of is ___________.
Correct answer is (2)
For a rolling spherical shell, we must consider the fact
that
it has both translational and rotational kinetic energy. The total kinetic energy
() can be expressed as the sum of the
translational kinetic energy () and the rotational kinetic energy
():
The translational kinetic energy of an object with mass (m) and linear velocity (v) is given
by:
The rotational kinetic energy of a rolling spherical shell with moment of inertia (I) and
angular velocity (ω) is given by:
For a rolling object without slipping, the relationship between linear velocity (v) and
angular
velocity (ω) is:
Where R is the radius of the spherical shell.
The moment of inertia for a spherical shell is given by:
Now, we can substitute the moment of inertia and the relationship between linear and angular
velocity into the equation for rotational kinetic energy:
Simplifying the equation:
Now, we can find the ratio of rotational kinetic energy to total kinetic energy:
Simplifying the equation:
Multiplying both the numerator and the denominator by 6:
Comparing this to the given ratio of , we can determine that the value of
is 2.
9. (JEE Main 2023 (Online) 8th April Evening Shift )
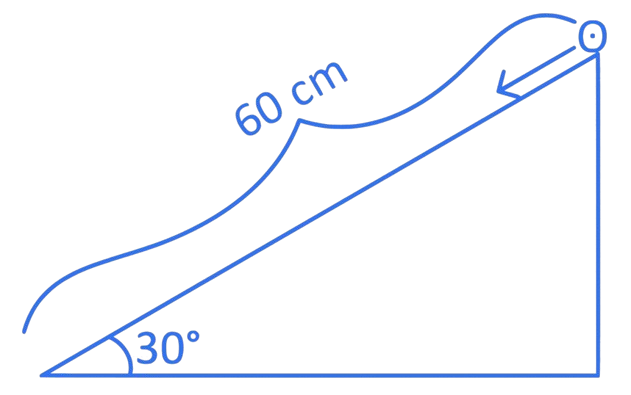
A hollow spherical ball of uniform density rolls up a curved surface with an initial velocity (as shown in figure). Maximum height with respect to the initial position covered by it will be __________ cm.
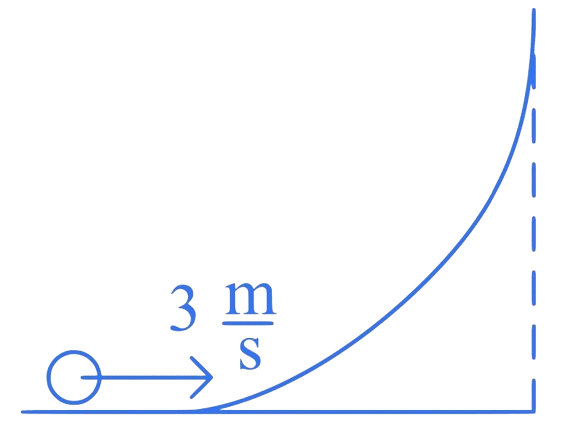
Correct answer is (75)
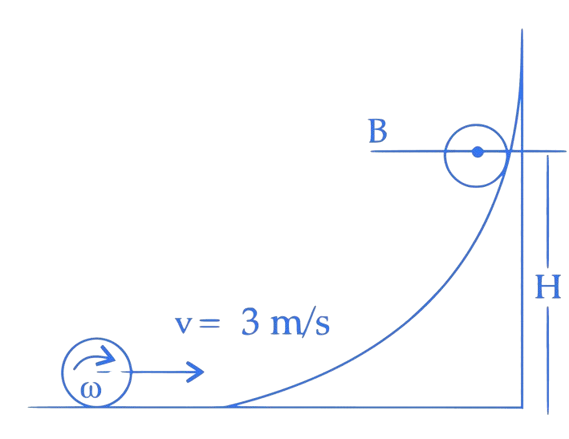
Total
initial kinetic energy
(for pure rolling)
Energy remains conserve during whole journey.
10. (JEE Main 2023 (Online) 1st February Morning Shift )
A solid cylinder is released from rest from the top of an inclined plane of inclination and length . If the cylinder rolls without slipping, its speed upon reaching the bottom of the inclined plane is __________ . (Given )
Correct answer is (2)
Loss in potential energy