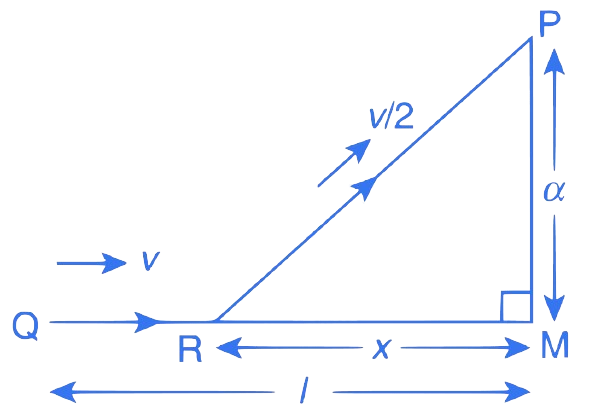
Correct Option is (C)
=
=
=
=
is antiparallel to
and it's direction towards the origin.
= 0
So
.