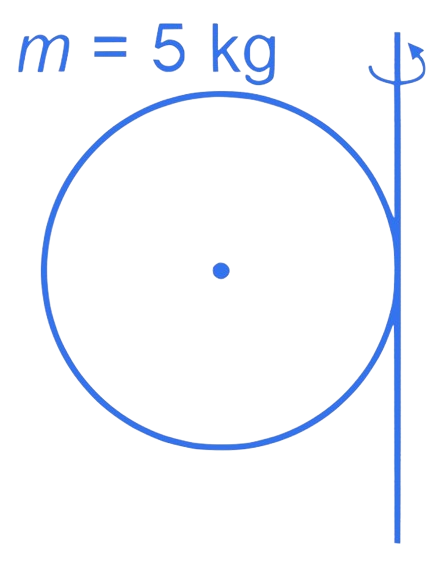
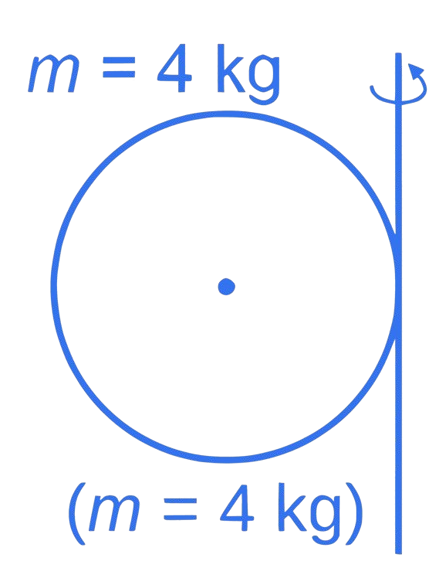
Correct answer is (176)

The moment of inertia of a system is the sum of the moments of inertia of its parts.

The moment of inertia of a solid sphere about an axis passing through its center is given by:

$I_{sphere}=\frac{2}{5}m{r}^2,$

where:

• $m$ is the mass of the sphere, and
• $r$ is the radius of the sphere.

The moment of inertia of a mass point about an axis is given by:

$I_{point}=m{d}^2,$

where:

• $m$ is the mass of the point, and
• $d$ is the distance from the axis.

Here, each sphere can be considered as a mass point located at the center of the sphere, and the axis is at the middle point of the rod.

The total moment of inertia of the system is the sum of the moments of inertia of the two spheres:

$I_{total}=2I_{sphere}+2I_{point}$

Substituting the given values:

$I_{total}=2\times (\frac{2}{5}\times 2\times (0.1{)}^2)+2\times (2\times (0.2{)}^2)$

This simplifies to:

$I_{total}=0.016+0.16=0.176{\text{ kg m}}^2$

So, the moment of inertia of the system about an axis perpendicular to the rod passing through its middle point is $0.176\times {10}^3{\text{ kg m}}^2$, or $176\times {10}^{-3}{\text{ kg m}}^2$.

Correct answer is (3)

$\begin{array}{rl}& \mathrm{I}={\mathrm{I}}_{\mathrm{cm}}+{\mathrm{Md}}^2\\ \\ & =\frac{{\mathrm{MR}}^2}{2}+{\mathrm{MR}}^2\\ \\ & =\frac{3}{2}{\mathrm{MR}}^2\\ \\ & \mathrm{x}=3\end{array}$

Correct answer is (5)

$m=\rho \pi R^{2}t$

$\begin{array}{rl}& \text{ so }{R}^2=\frac{m}{\rho \pi t}\\ \\ & I=\frac{m{R}^2}{4}=\frac{m^2}{4\rho \pi t}\end{array}$

So $\frac{I_1}{I_2}=\frac{{\rho }_2{t}_2}{{\rho }_1{t}_1}=\frac{5}{3}\times \frac{0.5}{1}=\frac{5}{6}$

So $x=5$

Correct answer is (3)

Kinetic energy of rod $E=\frac{1}{2}\frac{m{l}^2}{12}{\omega }^2$

or $\omega =\sqrt{\frac{24E}{m{l}^2}}=\sqrt{\frac{24E}{d\times A\times l^3}}$

$\Rightarrow \omega =\sqrt{\frac{24E}{dA{2}^3}}$

$=\sqrt{\frac{3E}{Ad}}$

So, $\alpha =3$

Correct answer is (5)

Solid Sphere :

$\begin{array}{rl}& I_{\text{tangent }}=I_{\mathrm{cm}}+m{R}^2\\ \\ & =\frac{2}{5}m{R}^2+m{R}^2=\frac{7}{5}m{R}^2\\ \\ & =7R^2(m=5\mathrm{kg})\end{array}$

CIRCULAR DISC :

$\begin{array}{rl}{I}_{\text{disc }}& =I_{\mathrm{cm}}+m{R}^2\\ \\ & =\frac{m{R}^2}{4}+m{R}^2\\ \\ & =\frac{5}{4}m{R}^2\\ \\ & =5R^2\end{array}$

$\frac{l_{\text{disc }}}{l_{\text{tangent }}}=\frac{5}{7}$

Concept :

1. For Solid Sphere :

Position of the axis of rotation : About its diametric axis which passes through its centre of mass


Moment of Inertia (I) = $\frac{2}{5}M{R}^2$

Radius of gyration (K) = $\sqrt{\frac{2}{5}}R$

Position of the axis of rotation : About a tangent to the sphere


Moment of Inertia (I) = $\frac{7}{5}M{R}^2$

Radius of gyration (K) = $\sqrt{\frac{7}{5}}R$



2. For CIRCULAR DISC :

Position of the axis of rotation : About an axis perpendicular to the plane and passes through the centre


Moment of Inertia (I) = $\frac{1}{2}M{R}^2$

Radius of gyration (K) = $\frac{R}{\sqrt{2}}$

Position of the axis of rotation : About the diametric axis


Moment of Inertia (I) = $\frac{1}{4}M{R}^2$

Radius of gyration (K) = $\frac{R}{2}$