Correct answer option is (B)
6. ⇒ (MHT CET 2023 10th May Evening Shift )
In a triangle , with usual notations, if , then value of is
A. 4
B. 16
C. 9
D. 25
Correct answer option is (B)
7. ⇒ (MHT CET 2023 10th May Morning Shift )
If one side of a triangle is double the other and the angles opposite to these sides differ by , then the triangle is
A. obtuse angled
B. right angled
C. acute angled
D. isosceles
Correct answer option is (B)
In , by sine rule,
According to the given condition,
In and
is right angled.
8. ⇒ (MHT CET 2023 9th May Evening Shift )
In and are in A.P., then
A. its altitudes are in A.P.
B. its altitudes are in H.P.
C. its medians are in G.P.
D. its medians are in A.P.
Correct answer option is (B)
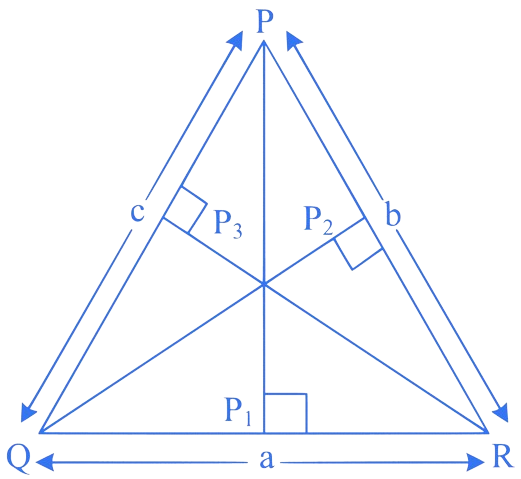
Let be the altitudes of Area of
Area
..... (i)
similarly,
..... (ii)
..... (iii)
By sine Rule,
Let
and are in A.P.
a, b, c are in A.P.
are in H.P. ..... (iv)
From equations (i), (ii), (iii) and (iv), we get and are in H.P.
9. ⇒ (MHT CET 2023 9th May Evening Shift )
Let be the lengths of sides of triangle such that . Then
A. 36
B. 32
C. 38
D. 40
Correct answer option is (A)
Adding above equations,
Solving equations (i), (ii), (iii), (iv) We get,
is right angled triangle
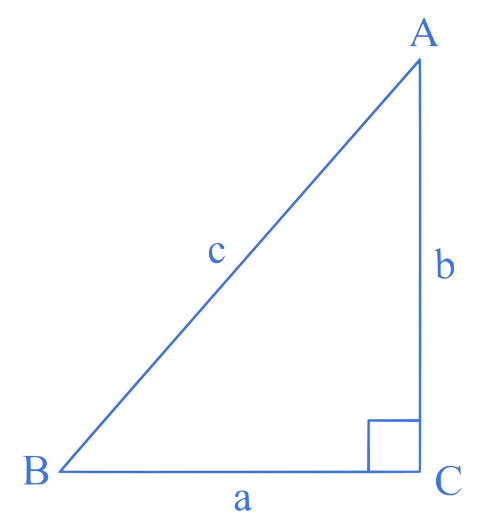
10. ⇒ (MHT CET 2023 9th May Evening Shift )
In , with usual notations, , if and are the roots of the equation , then
A.
B.
C.
D.
Correct answer option is (A)
Also,
Using , we get