Correct answer option is (D)
1. ⇒ (MHT CET 2023 12th May Evening Shift )
If
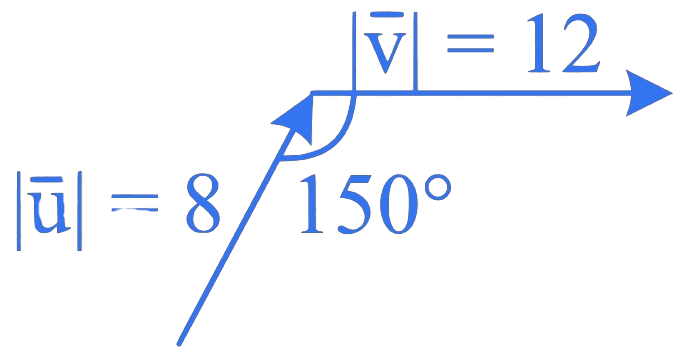
then
A. 96
B. 80
C. 42
D. 48
Correct answer option is (D)
2. ⇒ (MHT CET 2023 12th May Morning Shift )
If are three vectors, and , then the value of is
A. 2
B. 2
C. 1
D. 4
Correct answer option is (D)
If angle between and is and
Now,
3. ⇒ (MHT CET 2023 12th May Morning Shift )
Let be a vector parallel to line of intersection of planes and through origin. is parallel to the vectors and and is parallel to and , then the angle between and is
A.
B.
C.
D.
Correct answer option is (D)
Vector equation of the plane passing through the point and parallel to non-zero vectors and is
Plane is passing through the origin and parallel to vectors and
Equation of is:
Plane is passing through the origin and parallel to vectors and
Equation of is :
Note that is parallel to the cross product of and
Let be the required angle.
Angle between and
4. ⇒ (MHT CET 2023 11th May Evening Shift )
If the area of the parallelogram with and as two adjacent sides is . units, then the area of the parallelogram having and as two adjacent sides (in sq. units) is
A. 96
B. 112
C. 144
D. 128
Correct answer option is (B)
Area of the parallelogram with and as two adjacent sides is
Area of the required parallelogram
5. ⇒ (MHT CET 2023 11th May Morning Shift )
Let and . If is a vector such that and the angle between and is , then is
A.
B.
C. 1
D.
Correct answer option is (A)
Now,